医学部、難関大学受験対策としての数学の個別指導
このコンテンツでは、当塾のネット塾・WEB個別指導で指導として行っている科目・質問数無制限の説明指導・回答指導・添削指導について、当塾が誇る東大理三合格講師（東大医学部医学科）・東大「首席」合格講師陣の数学の個別指導の回答を特別公開していきます。これが医学部や難関大学に驚異的合格率を誇る当塾の充実指導の証拠です。
みなさんはやる気の問題や勉強効率の問題に悩まされたり、塾や予備校で一般的な問題解説講義を受けても自分のわからないところを解決できない、深く理解できない、ということを感じたことはありませんか？ これは多くの受験生が悩まされたり感じていることです。
でも、
■やる気や勉強効率を大きく阻害する「わからない」「できない」ところを日々解決していけるとしたら
■しかも、自分のわからない部分を圧倒的実力者が丁寧に説明してくれて理解していけるとしたら
■さらにそれが、受験数学を高いレベルで極めた人間のみがなしうる、他の問題にも通用する思考を伴った説明・解説とともに入試に必要なレベルで過不足なく得ていけるとしたら
■さらにさらに、受験数学のすべての問題を解きうる講師陣から、大学入試においてはここまで理解していれば大丈夫ですという明確な区切りとともに得ていけたら
あなたがやる気の問題に悩まされることは極限まで減ります。
→なぜなら受験勉強のやる気を阻害する最も大きな要因は「わからない」「できない」からです。
あなたが勉強効率に悩まされることはなくなります。
→なぜならこれ以上の効率を得ている受験生は日本全国にいないからです。
あなたの実力は確実に伸びます。
→なぜならこれ以上確実かつ効率的に実力を伸ばせる方法など存在しないからです。
当塾が、圧倒的実力講師陣を指導に当たらせている本当の効果や威力を体感してください。
みなさんが毎日の勉強でわからない問題やあいまいな部分をこのように解決していけるとしたらあなたの実力が伸びない原因はありますか？
以下に掲載するものはごくごく一部の質問と回答であり、1人の受講生がたった1回の質問回答で得られるものよりもはるかに少ない量です。当塾の受講生はここに掲載している回答を数学に限らず全教科、 1回に～10問程度、フリーコースの受講生は週に30～100問という量で得ていっているのです。これで実力が伸びないはずがないことはお分かりいただけると思います。
「受験生として実際に具体的に何を指導から得ることが出来るか、指導側がどの次元・レベルで実際何を与えているか」 このことは事実と異なるものを安易に語る人間がいる指導実績・合格実績や口先だけの仮装の実力や指導内容と異なり、決して操作することが出来ない事実、ごまかすことが出来ない事実です。
当塾が合格実績として掲載しているものは、受験戦略や勉強法や勉強計画だけを指導した受講生を一切含んでいません。 各教科の質問回答を継続的に数か月以上行った受講生しか合格実績として公表していません。 ですので一般の指導機関が出している合格実績に引き直せば当塾の合格実績は更なる驚異的な数字になります。
以下が受講生の実力が圧倒的に伸びる合格の天使の指導の秘密の一部であり、徹底した責任指導・個別指導であるがゆえに少数受講生でありながら国公立医学部医学科・旧帝大・難関大へ驚異的合格率を叩き出している事実と証拠です。
受講の有無にかかわらず、数学を効率的にマスターするために問題集や参考書にどう取り組んでいくべきなのか、何を得ていくべきなのかを具体例からしっかりと学んでください。 医学部や難関大学理系に合格するためには数学で高得点を獲得することが必須になります。
※実際に受講生からいただくご質問には教科書、問題集、参考書、過去問集の該当の問題の全文の画像がありますが、ここでは割愛させていただきます。
※ここに掲載する回答は、毎日受講生から頂く多くのご質問に対するごくごく一部をご紹介するものです。 すなわち、1人の受講生が1日に数問～10問程度の質問、１日トータルで百～数百問、1か月で数千～数万問、１年で数万～数十万問、数年で数十万～数百万問という膨大な数の質問回答の中からランダムに1問ずつ取り上げて掲載するものです。
※過去にブログに掲載したものを整理して掲載するとともに、 新たな質問回答をランダムに公開していきます。毎週更新予定です。覗きに来てください。
1.医学部受験塾：個別質問対応/勉強法講義/各教科エッセンス網羅講義
3.医学部受験のネット塾：全国の受験生に受験界最高峰の指導を！
4.フラッグシップネット塾：医学部受験のネット塾＋映像講義配信
ネット塾・WEB個別指導の数学問題の質問回答
受講生の数学に関する実際の質問と当塾講師陣の実際の回答を以下に掲載します。これらの質問と回答については実際に当塾のネット塾・WEB個別指導の受講生に掲載の許可をすべていただいています。
全国の受験生の皆さんのために提供を快く承諾してくださる当塾受講生の皆さんに、この場を借りてお礼を申し上げます。みなさんも大事なものを得てください。
平面図形
【平面図形に関するネット塾・WEB個別指導受講生の質問】
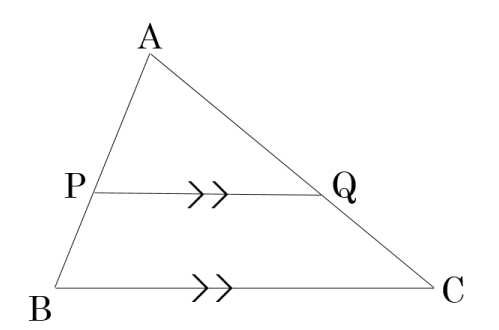
辺BC,PQは平行
△ABCの辺AB,AC上にそれぞれ点P,Qが存在する
この時、次のことが成り立つ
ただし、③の逆は成り立たない。
①BC∥PQ⇔AB:AP=AC:AQ
②BC∥PQ⇔AP:PB=AQ:QC
③BC∥PQ⇒AP:AB=PQ:BC
教科書等には一般にこのように書かれていますが、 「③の逆は成り立たない」のはなぜですか？
【東大理三合格（東大医学部医学科）講師 槇の回答】
図をまず見てください。
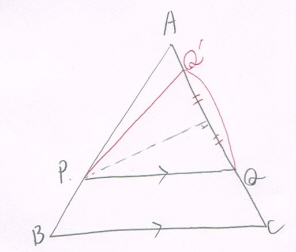
AP:AB=PQ:BCが成り立つとき、図のPQについては、確かにPQ//BCが成り立ちます。
しかし、AC上でPQ=PQ' となるような別の点Q'を取ることが出来るのです。
この場合、AP:AB=PQ':BC が成り立っていながら、PQ'//BC は成り立っていませんね。
このように反例があるため、逆は成り立たないのです。
極限
【極限に関するネット塾・WEB個別指導受講生の質問】
√(x^2 + x) + xのx→-∞の極限を求める際、x=-tと置き換えないで計算すると、
=(x^2 + x - x^2) / [√(x^2 + x) - x ]
=x / [√(x^2 + x) - x ]
= 1 /[√(1 + 1/x) - 1 ]
となり、極限が1/(1-1)=1/0になってしまい、置き換えた場合と解答(-1/2)と異なってしまいます。なぜそうなるのかわかりません。
【東大理二「首席」合格（東大医学部医学科）講師 大久保の回答】
非常にいい質問であり、とても多くの受験生が間違えるところであります。 以上の式変形をしていただいたのだと思いますが、どこが誤りなのでしょうか。
√(x^2 + x) + x
=(x^2 + x - x^2) / [√(x^2 + x) - x ]
=x / [√(x^2 + x) - x ]
ここまでは何の問題もありません。問題はこの後
= 1 /[√(1 + 1/x) - 1 ]
としたところです。ここが誤りです。
x / [√(x^2 + x) - x ]の分母をxで割って、
1 / [√(x^2 + x) / x -1]とし、√の中に1/xを入れて1/x^2として
1 / [√[(x^2 + x)/x^2] -1]
としたのだと思いますが、これが誤っているところです。
今、x→-∞を考えているので、x<0です。負の数は√の中に入れることができません。
x / [√(x^2 + x) - x ]
= 1 / [√(x^2 + x) / x -1]
ここまではいいですが、このあとxを√の中に入れる際にそのままでは入れることができません。
そこで、xが負の時-xなら正ですので、-xを中に入れます。
√(x^2 + x) / xにおいて、x=-(-x)として、この(-x)を中に入れます。
√(x^2 + x) / -(-x)
=- √(x^2 + x) / (-x)
=- √[(x^2 + x)/(-x)^2]
=- √(1+1/x)
となります。
1 /[ - √(1 + 1/x) - 1 ]
となりますから、x→-∞とした時この極限値は1/(-1-1) = -1/2となり、置き換えた場合と一致します。
このように√の中に負の数を入れる時には、そのままでは入れられないというのをよく忘れます。
私たちは負の数の操作に想像以上に慣れていません。
このようなミスを防ぐために、原則的にx→-∞の時にはもうt=-xと置き換えてしまうのが安全だと言われています。
確率 排反と独立
【確立についてのネット塾・WEB個別指導受講生の質問】
確率の分野なのですが、排反と独立の違いが明確にわからないです。
明確な違いを教えてください。
【東大理三合格（東大医学部医学科）講師 安藤の回答】
排反と独立は、確率を求めるときにキーになる二つの考えですね。この二つは、実際全く異なる概念です。定義と具体例を確認しましょう。
排反というのは、いくつかの事象が同時には起こらないことを言います。AとBが排反なら、AかつBが起こる確率は0です。例えばコインを投げて表がでる事象と裏が出る事象は排反です。
一方で、独立というのは、高校数学だと多くは「試行」に対して使われてそれぞれの試行が関係しないこと、互いに試行の結果に影響を及ぼさないことをいいます。試行aとbが独立と言われたら、aの結果がどうであろうと、bの結果には影響しません。
例えばガチャポンで1回目に出たものが低レアの景品だった場合、2回目は高レアの景品が出る確率が高まります(分母が減るからです)。この場合は1回目と2回目は独立ではありません。一方で、ソシャゲ（ソーシャルゲーム）の電子ガチャの場合は、何度回しても高レアの排出率は一定ですから、この場合1回目と2回目は独立な試行ということになります。
確率を求める文脈では割と同格に扱われることが多いので混乱してしまうのかも知れません。ですが定義を確認すれば、上のようにかなり違う概念なんだと分かってもらえると思います。実際に問題を解くときにも、どちらを使えばいいか分からなくなったら定義に戻って考えるといいでしょう。
次数がわからない関数を含む恒等式の場合分け
【恒等式の場合分けに関するネット塾・WEB個別指導受講生の質問】
[問題]
n次式であるｆ（x）が
(ｘ+1)ｆ '(ｘ)-3ｆ(ｘ)+2ｘ-1=0
ｆ(0)=1
という関係を満たしているとき、ｎとｆ(ｘ)をそれぞれ求めよ。
この問題を解くとき、ｎと１の大小で場合分けをする必要があります。
では、なぜその場合分けをしなければならないか説明することができますか？
[受講生の実際の質問]
nと1の大小で場合分けをするというのが理解できていません。
【東大理三合格（東大医学部医学科）講師 槇の回答】
一般に、n次式を微分するとn-1次式になります。よってf(x)がn次式ならf '(x)はn-1次式です。 これは大丈夫ですね。
本問のように次数のはっきりしない恒等式の問題では、最高次数の項を比較するのが常套手段です。
(x+1)は1次式ですから、(x+1)f'(x) は1+(n-1)=n次式、-3f(x)はn次式、2x-1は1次式です。
したがってn≧2であれば、最高次数であるn次の項をもつのは(x+1)f'(x) と-3f(x) ですから、この２項について、それを展開した中でのn次の項を比較すれば済みます。
しかしn=1のとき、最高次数である1次の項をもつのは、(x+1)f'(x) , -3f(x) のほかに2x-1も含まれます。 よって比較すべき項が増えます。
このように、n=1とそれ以外の時で、最高次数の項を比較する際考慮する項が異なるので、場合分けをしなければいけません。
因数分解
【因数分解に関するネット塾・WEB個別指導受講生の質問】
2cos2x + 8sinx -5 ≦0
を因数分解したあと
(2sinx-3)(2sinx-1)≧0
からわからなくなってしまいました。
【東大理二「首席」合格（東大医学部医学科）講師 大久保の回答】
非常に良い質問です。
少し戻って、
(2sinx-3)(2sinx-1)≧0
から説明しましょう。ここから実は2つの考え方があります。
1つ目は以下のようなものです。
2sinx-3の符号について考えて見ましょう。
sinxはどんなに頑張っても最大値1までしかいけません。ということは、
2sinx-3の最大値は-1ということです。つまり、2sinxは常に負です。
よって、(2sinx-3)(2sinx-1)≧0
というのは、常に2sinx-3<0であることを考えると両辺を2sinx-3で割ることができて(0ではない、かつ符号がわかってるので不等号の向きの変化がわかるため)
2sinx-1≦0となります。
あとはここからsinx≦1/2として解いていけば良いです。
さて、2つ目は○○さんのやっていただいたように、
(2sinx-3)(2sinx-1)≧0から
sinx≦1/2 または sinx≧3/2
とするものです。(この「または」が地味に大事です。意識していましたでしょうか？)
sinx≦1/2を満たすxは0≦x≦π/6または5π/6≦x<2πで良いと思います。
sinx≧3/2をみたすxはどうでしょうか？
上述の通り、sinxはどんなに頑張っても最大値は1までしかいけません。よって、sinx≧3/2をみたすxは存在しない、というのが正しいです。
数列の一般項
【数列にするネット塾・WEB個別指導受講生の質問】
{an},{bn}の一般項をそれぞれan=2^n, bn=3n+2とする。{an}の項のうち、{bn}の項を小さい方が順に並べて得られる数列{cn}の一般項を求めよ。 という問題で、模範解答が途中からわからなくなりました(実際にはより具体的にその箇所が指摘されています)。
【東大理二「首席」合格（東大医学部医学科）講師 大久保の回答】
2つの数列 an = 2^n bn = 3n+2
のうち、一致している項のみを取り出すと一般項はどう書けるかという問題です。
この場合は、まずanの何項目とbnの何項目が一致しているかを調べる必要があります。 それがわかれば、あとはそれをanかbnのどちらかの式に代入すればcnが求まります。
よって、今anのl項目がbnのm項目に等しいとしてlとmの関係を求めます。
al = bmですから、
2^l = 3m+2です。
さて、これをこのまま解こうとすると左辺は指数関数、右辺は1次式で解くのが難しいです。
そこで、直接求めるのが難しい場合は実際の数から予想してから方針を立てるという鉄則に従いましょう。
少しanとbnの項を書き出してみましょう。
an = 2, 4, 8, 16, 32, 64, 128
bn =5,8,11,14,17,20,23…,32…
よって、かなり雑ではありますが、8,32が一致してますのでもしかしたらanの項が1個おきに一致しているのではと思います。 そこで、実際に128も一致しているかをみると、 128=3n+2 を解けばn=42とできますので、bnも48項目に128があり、一致してます。
いよいよanの一個おき(初項は8)にanとbnが一致していそうなので、これをcnと予想します。
cn=8,32,128,…つまり、cnは初項は8、公比は4の等比数列と予想できます。
あとは、これを証明するだけです。
i) 初項8は一致している。
ii) anのl項目とbnのm項目が一致していると仮定した時、anのl+2項目もbnのどこかに一致していることを示す。
al = bmですから、
2^l = 3m+2です。この時、
al+2
= 2^(l+2)
= 4× 2^l
= 4× (3m+2) (仮定を使った)
= 12m + 8
= 3(4m+2) +2
よってal+2 = b4m+2なので、確かに一致する項がある。
ゆえに、anのl項目とbnのm項目が一致していると仮定した時、anのl+2項目もbnのどこかに一致していることが示された。
i)ii)より、数学的帰納法からcnは初項8、anの2つおきの項からなることが求まり、cnは初項は8、公比は4の等比数列とわかったので一般項は
8×4(n-1)
=2^(2n+1)
このように、模範解答には予想して数学的帰納法というのがはっきり書いてなかったので分かりにくかったのだと思います。 実際には上記のような思考過程を経ています。
漸近線の変化
【漸近線のネット塾・WEB個別指導受講生の質問】
190、192の画像についてです。これらの問題は正の無限大と負の無限大によって、漸近線が変化する問題ですが、この手の曲線であることの判別は、実際に極限を取らないとわからないものなのでしょうか？
※実際の受講生の質問には問題集の問題の画像が添付されていますがここでは割愛させていただきます。
【東大理三合格（東大医学部医学科）講師 槇の回答】
大体の推測をすることはできます。要は、具体的にxに「大きい値」を代入してみて、定数を無視すればどうなるかを考えれば良いのです。
190なら、x=100などを代入してみると、√の中身は、-1などは無視できるので√x^2=x となりますよね。ということはxが十分大きければ2x+x=3xに近づきます。
負ならどうかというと、x=-100 にすれば√の中身は、やはり-1は無視出来て、√(-100)^2=100=-x となります。
よって2x-x=x に近くなるわけです。
常にこのように推測できるわけではないですが、√の中身にx^2が入っている今回のような関数は、上の方法で推測できる場合が多いと思います。
複接線
【複接線のネット塾・WEB個別指導受講生の質問】
204の画像についてです。ここでは複接線というものが取り上げられていますが、これは入試でよく取り上げられるのでしょうか？また対処の仕方としては、どういったものになるのでしょうか？
※実際の受講生の質問には問題集の問題の画像が添付されていますがここでは割愛させていただきます。
【東大理三合格（東大医学部医学科）講師 槇の回答】
複接線という言葉自体はどうでも良いですが、たまに取り上げられることはありますね。 といっても「２点で接する接線の方程式は」とか、しっかり明記されると思います。
今回のような問題で「実は複接線があるから本数≠接点の個数でした～」みたいな落とし穴を作るのは、 難関大学の中でさらに難しい問題で、可能性がある程度の話です。
なのであまり心配しなくても良いですが、グラフの概形を考えられるなら、 一度確認してみるとより盤石ではあります。
積分 面積の最小
【積分 面積の最小に関するネット塾・WEB個別指導受講生の質問】
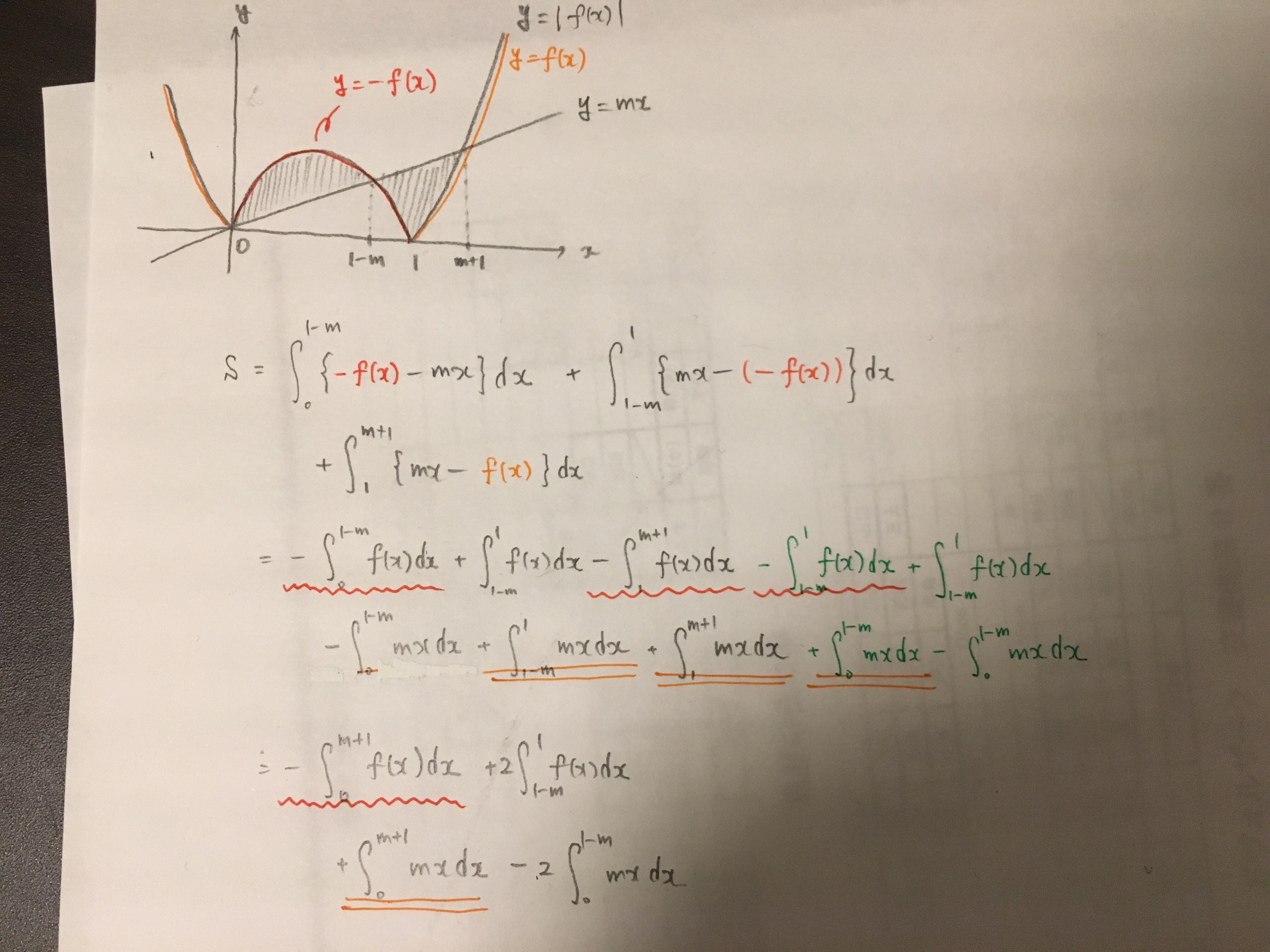
曲線 C : y = |x(x-1)| と 直線 l : y = mxがある。C と l とで囲まれる部分の面積 S を最小とする m の値を求めよ。ただし、C と l は異なる３つの共有点を持つ。
という問題ですが、解説にある一連の式変形が少しこんがらがってしまいます。
この式変形はどうなっているのでしょうか。
【東大理三合格（東大医学部医学科）講師 深川の回答】
添付図を参考にしてください。落ち着いて考えましょう。
計算を楽にする工夫です。あと少しで積分範囲が全部繋がって綺麗になるのに…と思っているとこの式変形を思いつきます。
複素数 虚数ωの範囲
【虚数ωの範囲に関するネット塾・WEB個別指導受講生の質問】
「数学２Bの虚数ωの範囲を、学校では「入試にはほとんどでないからやらなくていい」
と言われたのですが、本当にやらなくていいのでしょうか？」
このコンテンツをご覧いただいている皆さんに質問です
この質問ですが、みなさんが今受けている指導や質問できる人に質問した場合、的確な回答が得られますか？
またみなさんも他の科目や分野でこのような疑問を持ったことはないですか？
安易に語られているゴールから逆算するとか志望校の過去問を見ればわかるというような指導、アドバイスではこの問題には的確に回答できません。
的確なものは絶対に得られません。
【東大理三合格（東大医学部医学科）講師 槇の回答】
ωについては、説明なしで出題されることは無いと思います。
しかし「x^3=1の虚数解をωとする」といった説明があって、それに関する
出題がされるというのは大いにありえます。
また、ここでポイントとなることは、ωに限らず他の複素数でも有用です。 「次数下げ」というテクニックになりますが、応用できますか。
例えば下の問題を解いてみてください。
a= - 1+√2 i とするとき、a^4 の値は？
ヒント：まともに計算しようとすると大変ですね。
そこで、「aが解となる２次方程式」を求めてみてください。
そうすれば28(2)と同じように次数を下げることが出来ます。
回答掲載解説
このような回答を得られるかどうかだけでも今後の勉強や受験対策に相当な差がつくことはお分かりいただけると思います。
みなさんもこのような部分で疑問を持ち、まだ基礎標準知識の習得が済んでおらず過去問分析が自力でできない段階では、質問できる人にしっかり聞いてください。
「試験にはでない」というのなら他の分野に絡んでこないのか、直接出ないとしても数学的思考としてたの分野でも必要になるものではないのかという部分まで突っ込んで質問することで的確なものが得られます。
ここではっきりと真実をお伝えしておきますが、大学入試において何をどこまで得ておけばいいか、考えておけばいいのかという線引きを明確にできるのは、またそれらを踏まえた的確な戦略や勉強法、勉強計画を指導できるのは以下の条件を満たす場合のみです。
2、実際に基礎理論から具体的問題にわかりやすく解答できること
3、実際に全国の大学のどんな問題にも的確に解答できること
という3段階のレベルをすべてクリアーしている実力を有している場合のみです。
もちろん自称ではなくしっかりとした受験結果に実証されていることが大事ということも忘れないでください。
戦略や勉強法や計画だけ語ることは、拝借して行けばいくらでも圧倒的実力者と同じことを語れます。
しかしそれは決して的を射た的確なものではないことは本来説明するまでもないことです。
難関大学の数学や物理、化学、生物など理系学部の具体的な問題について基礎理論から解説・解答できないにもかかわらず、
また自身が実際にその次元での合格という結果を出していないにもかかわらず、
戦略や勉強法、勉強計画だけが優れたものになることなど絶対にありえません。
自身の受験結果に実証されている高い実力がある指導者から指導を得られるか否かだけで、実際の勉強効率、成績の伸び、さらには狭き門である医学部や難関大学の合否まで決まっている側面があるのも事実です。
今回はちょっと本音をお伝えしました。
本気になって合格へ向かってください。
次回以降へ続く・・・・・
数学も含め全教科質の高い個別指導が受けられる圧倒的実力指導
医学部・難関大学合格のためには数学を得意科目にすることがマストです。そのためには質の高い個別指導をうけることができるなら圧倒的に有利」になります。この点は予備校さんの指導との比較検証も必要ですので「医学部受験に予備校は不要？5つのチェックポイント」のページもご覧ください。
他指導では決して得られない医学部・難関大学合格に直結する優れた指導をご提供しているのが当塾指導です。指導内容や詳細を皆さんの目で是非検証してください。
医学部受験塾：個別質問対応/勉強法講義/各教科エッセンス網羅講義を行うリアル塾
■あなただけの「合格計画」「合格戦略」の策定、問題集・参考書の選定
■各教科の受験戦略・勉強法講義＆指導
■全教科の個別質問対応：説明指導・回答指導・添削指導
■毎週定期の進捗報告でモチベーション維持と理解確認の逆転授業(講師槇の造語)
■「英語」「数学」「国語」「物理」「化学」「生物」の生講義＆映像講義
難関大学受験塾：個別質問対応/勉強法講義
■あなただけの「合格計画」「合格戦略」の策定、問題集・参考書の選定
■各教科の受験戦略・勉強法講義＆指導
■全教科の個別質問対応：説明指導・回答指導・添削指導
■毎週定期の進捗報告でモチベーション維持と理解確認の逆転授業(講師槇の造語)
医学部受験のネット塾：全国の受験生に受験界最高峰の指導を！
■あなただけの「合格計画」「合格戦略」の策定、問題集・参考書の選定
■各教科の受験戦略・勉強法講義＆指導
■全教科 質問数無制限で説明指導・回答指導・添削指導
■Skypeを用いた毎週定期の進捗報告でモチベーション維持と理解確認の逆転授業(講師槇の造語)
フラッグシップネット塾：医学部受験のネット塾＋映像講義配信
■あなただけの「合格計画」「合格戦略」の策定、問題集・参考書の選定
■各教科の受験戦略・勉強法伝授
■全教科 質問数無制限で説明指導・回答指導・添削指導
■Skypeを用いた毎週定期の進捗報告でモチベーション維持と理解確認の逆転授業(講師槇の造語)
■受験戦略・勉強法講義配信
■センター試験高得点戦略対策講義各教科配信
■ミニ・マックスメソッド講義（2次・私大対策エッセンス網羅講義）各教科配信
高校1，2年生のためのリアル塾：医学部・難関大学合格への礎を築く
■あなただけの「合格計画」「合格戦略」の策定、問題集・参考書の選定
■各教科の受験戦略・勉強法講義＆指導
■全教科の個別質問対応：説明指導・回答指導・添削指導
■毎週定期の進捗報告でモチベーション維持と理解確認の逆転授業(講師槇の造語)
高校1，2年生のためのネット塾：医学部・難関大学合格への礎を築く
■あなただけの「合格計画」「合格戦略」の策定、問題集・参考書の選定
■各教科の受験戦略・勉強法講義＆指導
■全教科 質問数無制限で説明指導・回答指導・添削指導
■Skypeを用いた毎週定期の進捗報告でモチベーション維持と理解確認の逆転授業(講師槇の造語)
※今後もコンテンツを追加して行きます。お友達やお知り合いと適切な情報を共有し切磋琢磨しあうことは、あなたの合格可能性を高めることに非常に役立ちます。実はこのこと自体が難関大学合格者に共通した受験対策の特徴でもあります。以下のシェアボタンを押せば簡単にシェアできます。
