医学部合格へ導く物理の個別指導
医学部に合格するためには、物理でできるだけ安定して高得点を獲得することが戦略的に重要になります。 多くの医学部合格者は物理を時間短縮と得点源科目にしている事実があります。
例外として、一部の単科の医科大学や私大医学部の物理の問題は、誰も解けない問題=解く必要がない問題=かかわってはならない問題=悪問もしくは教授の趣味と言える問題、 が存在しています。このような医学部を志望する場合、そういった類の問題に以下に関わらないで出来るだけの高得点を獲得するかという知識と選別方法の確立が重要となります。
以下では、当塾が指導として行っている科目・質問数無制限の説明指導・回答指導・添削指導について、 当塾が誇る東大理三合格講師・東大医学部医学科）講師陣の実際の 物理の質問に対する個別指導の回答を掲載します。 これが医学部に驚異的合格率を誇る当塾の充実指導の証拠です。
次の視点をもってご覧ください。
■あなたはこの受講生のような充実した勉強を出来てますか？
■実際にこのような質問回答指導を毎週、毎日受けている受講生と数か月後にどのくらいの実力差がついているか想像できますか？
■予備校の授業を単に受けているだけでこれだけの自分の疑問点、弱点部分を的確にピンポイントでダイレクトに効率的に毎日補強できますか？
■家庭教師の1回2時間の指導でこれだけの量の質問回答指導を得られますか？
■またこれだけの次元・質・レベルの的確な回答指導を得られますか？
■あなたは数か月後このような受験生と狭き合格枠を争うのです。
当塾の受講生はこのような回答指導を毎週毎週～10問、フリーコースの方は数十問という数で得ていっているのです。 年間にしたら１人数百、数千という数になります。
「受験生として実際に具体的に何を指導から得ることが出来るか、指導側がどの次元・レベルで実際何を与えているか」 このことは事実と異なるものを安易に語る人間がいる指導実績・合格実績や口先だけの仮装の実力や指導内容と異なり、決して操作することが出来ない事実、ごまかすことが出来ない事実です。
以下が受講生の実力が圧倒的に伸びる合格の天使の指導の秘密の一部であり、徹底した責任指導・個別指導であるがゆえに少数受講生でありながら国公立医学部医学科・旧帝大・難関大へ驚異的合格率を叩き出している事実と証拠です。
受講の有無にかかわらず、物理を効率的にマスターするために問題集や参考書にどう取り組んでいくべきなのか、何を得ていくべきなのかを具体例からしっかりと学んでください。
物理の個別指導の実際の質問回答
注意１
実際に受講生からいただくご質問には教科書、問題集、参考書、過去問集の該当の問題の全文の画像がありますが、ここでは割愛させていただきます。
注意２
ここに掲載する回答は、毎日受講生から頂く多くのご質問に対するごくごく一部をご紹介するものです。
すなわち、1人の受講生が1日に数問～10問程度、受講生トータルで１日に数百問、1か月で数千～数万問、１年で数万～数十万問という膨大な数の質問回答の中からランダムに取り上げて掲載するものです。
回析格子の考え方
受講生の質問
回折格子ではたくさんの光が回折しているのに、隣り合う光が強め合う条件だけを考えるのはどうしてですか？
東大理三合格｜東大医学部医学科講師 槇の回答
「スクリーン上のある一点に集まる光が、一番強め合うのはどんなときか」を考えます。 もちろん、隣り合う光でなくて、２つとなりとか３つとなりとかと強め合うときもあります。 しかし、一番強くなるのは、隣同士の位相差が２πの倍数であるために、 すべての回折光が足し合わさる場合です。そうなる場合を考えているわけですね。
ニュートンリングや薄膜などの干渉で覚えておくべきこと
受講生の質問
ニュートンリングや薄膜などの干渉で、明線・暗線の条件式は覚えたほうが良いですか？
東大理三合格｜東大医学部医学科）講師 槇の回答
式を覚えておく必要は全くありません。むしろ、入試ではいろいろなパターンや設定で問われるので丸覚えは役に立ちません。
そうではなく、経路差を求める→強め合う/弱めあう条件を求める という一連の計算過程を自分でできる必要があります。
なので、覚えておくとすれば、「ニュートンリング・くさびなどにおける経路差の求め方」ですかね。 これらは一回求め方を見ておく必要はあると思います。もちろん、ただ式を覚えるのではなく、方法を覚えるのです。
あとはどんな干渉の問題も上で書いた過程は共通です。 それと「屈折率小→大の反射では位相がπずれる」というのは覚えておいたほうが良いと思います。
光の固定端反射・自由端反射
受講生の質問
光の固定端反射・自由端反射というのがよくわかりません
東大理三合格｜東大医学部医学科講師 槇の回答
屈折率小さい媒質→大きい媒質の反射は固定端＝πずれる
屈折率大きい媒質→小さい媒質の反射は自由端＝位相ずれない
と覚えてください。
イメージとしては、屈折率大きい物質は「硬い物質」と考えます。
やわらかい物質を進んできた光が硬い物質にあたると、ガキンと反射されるイメージはできますよね。
この場合硬い物質は「動かない壁」と考えて固定端と捉えられます。
硬い→やわらかい物質なら逆に、やわらかい物質はふにゃふにゃ動くイメージなので自由端なのです。
斜めのドップラー効果
受講生の質問
図のように、音源をのせた車が一定の振動数foの音を出しながら直線道路を一定の速さvで走っている。観測者Aは道路のすぐ脇で、観測者Bは道路から距離dの地点で静止して音を聞いている。風はないものとし、音速をVとする。 以下の問いに答えよ。
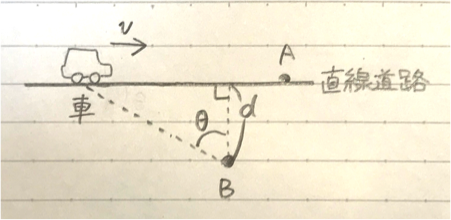
(あ) 図のように、車が観測者Bから見てθの方向にあるときに発せられた音が、Bに到達した時に観測される振動数を、V , v ,θ, F0 を用いて表せ。
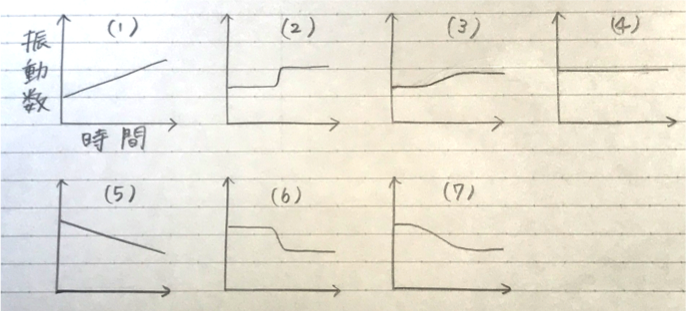
(い) 車が十分に離れた場所から観測者Aに近づき、十分に離れた場所に到達するあいだに、A , B が聞く音の振動数の時間変化のグラフとして最も適しているものを次のうちからそれぞれ選んで答えよ。ただし、重複して選んではいけない。
東大理三合格｜東大医学部医学科講師 江尻の回答
この問題を見てみると、（あ）では観測者に対して直進してくるのではない音源による（つまり斜めの）ドップラー効果となっています。
どう解くかというと、音源の進んでいる直線上に観測者がいる場合の公式f={(V-w)/(V-v)}f_0（wは観測者の速度、vは音源の速度）を使えば大丈夫です。 この際、音源（車）と観測者（B）を直線で結び、それぞれの速度の直線の向きの成分をwとvに代入すれば良いのです。
今回は観測者は動いていないのでw=0、音源の速度vのこの直線方向の成分はBの向きにvcosθなので、 これを公式のvに代入すればOKとなり、結局答えは(V/V-vsinθ)f_0となります。
大事なことは、観測者と音源を結んだ方向の成分だけを取り出すということです。 斜めでないドップラー効果の問題でこの方法で考えても、観測者と音源がいる直線上を両者が動いているので、 その方向だけ速度の成分を取り出しても同じ値になるので問題ないですね。
ちなみに（い）も解くと、こうなります。 まず、Aについては、音源が自分のいるところを通り過ぎるまでは振動数はf_0より大きい一定値（(V/V-v)f_0）、 通り過ぎてからはf_0より小さい一定値（(V/V+v)f_0）と考えられるので、それっぽくなっている（6）になります。
Bについては、（1）の答えであるf=(V/V-vsinθ)f_0・・・★を使って考えます。 これの面倒くさいところはθが時間によって変わるので変化が連続的になりそうだというところです。 Aの場合は音源が通り過ぎる瞬間にパッと変わるのですが、Bの場合はそうもいきません。
しかし、車が右へ進む（時刻tが進む）とだんだんθが小さくなる（単調減少する）のでfも小さくなることが★からわかりますね。 この時点で（5）と（7）に絞れます。問題は、下がり具合がどう変わるかですね。例えば（5）の図では、どの時刻でも下がり具合が一定です。 下がり具合を調べるには、θと時刻tの関係を見れば良いです。
車がまだ左のとても遠くにある時とBの近くまで来た時を比較すると、 同じ時間間隔（同じ距離の移動）でも遠い時の方がθの変化が小さいことがわかります（図を描いてみましょう）。 なので、fの変化（＝下がり具合）も同じ時間間隔をとってみると車が遠い時の方が近い時より少なく、この状況を表しているのが（7）ですね。
補足：（6）がなぜ本当に通り過ぎた瞬間にパッと変わるのではなく少し曲線的になっているかというと、Aは道路の「すぐわきに」いるのであって本当に道路のど真ん中に立っているわけではないからです（車にひかれてしまいますからね）。なので大体パッと変わっているように見える、激しめの角度の曲線になっているというわけです。
力のつり合いが成り立つとき
受講生の質問
ちょっと気になったことがありました。 エッセンスに運動している物体が一瞬静止したときには力のつり合いはだめで完全な静止状態で力はつり合うとありました。あたりまえといえばあたりまえなのですが、それはどうしてですか？
【東大理三合格（東大医学部医学科）講師 槇の回答メール】
運動方程式（質量）×（加速度）＝（物体に働く力） を想起してみるとわかりますが、力のつり合いが成り立つかどうかは、その物体の速度ではなく、加速度で判断すべきなのです。
物体が一瞬停止して速度が0になっても、加速度は0であるとは限りませんよね。
（例えばボールを上に放り投げるとき、最高点で一瞬停止しますが、重力加速度は常に働いています。）
こういった場合は、上の運動方程式の左辺は0になりませんので、力のつりあいは成り立ちません。
物体の加速度が0で、運動方程式の左辺が0になるからこそ、0=（物体に働く力の総計）、すなわち力のつりあいが成立するのです。
物理を得意科目にして医学部合格を引き寄せる！
以上が回答ですが、みなさんは、質問しても的確な回答が得られない、 回りくどい説明をうけて結局「うーん・・・・そうなのか・・・・・」 という感じ、という指導を受けていないでしょうか。
以上に掲載した質問回答は、簡単な例示にすぎませんが、 科目を問わず基本原理や基礎理論に基づいていない説明や知識というのは、 場当たり的にその説明や理解の数だけ覚えるべきことや理解すべきことが増えていってしまいます。
その結果どんなに勉強しても知識が体系化しない、 本質的理解が伴わない勉強になってしまいます。 その結末が初見の問題に対処できない、応用問題に対処できないということになるのです。
これは当たり前ですよね。 だって多くの問題を場当たり的にその解説や説明を覚えている、 理解しているに過ぎないのですから。 問題の数だけ説明や理解が存在してしまうことになるのです。
これとは逆に、上記回答のように基礎理論・基本原理からの核心をついた説明であるならば、 それは的確にかつ回りくどい説明などせずとも理解・納得を導くことが出来るのです。 そして自分で考えて応用もきくようになっていくのです。
その証拠が上記受講生が上記回答を得て理解した後、 「このあいだ質問した力のつり合いについて確認なのですが、等速運動をしているときは力はつりあっているというのも加速度が０で運動方程式の左辺＝０になるからということですよね？」
という理解を確認する質問に変わるのです。
みなさんも是非、表面的に理論を語るに過ぎない勉強法ではなく、 具体策・具体的方法論としての理論をどんどん得ていってください。
これは自分でわからない部分はどんなに考えても時間の無駄ですし、 的確なものは得難いですし、気づけないものは気づけませんので、 質問できる人にどんどん質問していってください。
理解の上にしか理解は重ならない、すなわち応用力はついていかないのです。
土台である部分の基礎に曖昧・不明確な部分があれば、 そこから派生するすべての理論、問題はすべて曖昧・不明確な解答しか導けないということです。
今のうちに自分の勉強を見直してみてくださいね。
曖昧・不明確な理解の上にこの先どんなに勉強を重ねようが、 どんなに頑張っても成績はそこそこまでしか伸びないという現実を あなた自身の合格のために明確に認識してください。
次回以降へ続く・・・・・
