数学勉強法を東大「医学部」「理三」合格者30名超が具体的対策と共に解説

【数学勉強法の全体像】基礎・標準問題集及び過去問集それぞれの使い方

詳細な数学勉強法の解説に入る前に、まずは数学の基礎・標準問題集及び過去問集のそれぞれの学び方の全体像を解説した動画をご覧ください。

数学の勉強法としてどの問題集・参考書も何度も繰り返す的な勉強法が語られますが、これは問題集のレベルに応じた役割を理解していない勉強法です。このような勉強法を実践していても目的がずれてしまい得るべきものを得られません。すなわち、実力は効率的に伸びません。

今回はこの点について地方公立高校⇒東大理三現役合格講師正門が解説した動画をプレゼントします。 今回の動画の内容は当塾の著書、
受験の叡智【受験戦略・勉強法の体系書】 ▶
医学部受験の叡智【受験戦略・勉強法の体系書】▶
に詳しく記載してあります。

この動画をご覧いただいた後、再度読み直してください。 本当の意味を理解していただけると思います。 これによりあなたの日々の勉強は効率化するとともに実力が伸びます！ 必ず読み直して復習してくださいね。

数学勉強法の３大要素

数学の実力をあげる勉強法として大きな柱が３つあります。

以上の3つです。

数学の勉強として大事になるのは、この大きな3つの柱で勉強法を捉えることです。 そして各段階を決してスキップしないことです。 以下ではこの区分けに従って数学勉強法を解説していきます。

基礎習得段階における数学勉強法と対策ポイント

基礎の習得段階における数学勉強法のポイントは、教科書（もしくはそれに代わる代用書）と その傍用問題集（もしくはそれに匹敵するレベルの基礎問題集）をどのように学び、使っていくかです。

この基礎の習得過程だけを見ても世の中には間違った数学勉強法が氾濫しているので注意してください。

教科書の使い方

地方私立高校⇒東大理三現役合格講師 深川（センター試験869/900）

数学は基礎の段階の習得が一番大切です。 これはもちろん別の教科についても同じことがいえるのですが、数学については特にこの段階が大切です。

数学の基礎の習得では教科書もしくはそれに準じた参考書と、基礎的な問題集を用います。 教科書や参考書は自分の持っているものを用いれば問題ないかと思います。

数学の教科書は実にわかりやすく書かれており、教科書の例題を読み解いていくだけでも相当な力になります。 また、数学ではインプットよりもアウトプットの方がはるかに重要です。

これはつまり、問題の解答を眺めているだけでは一向に問題を解けるようにはならないという意味です。 教科書の例題を読み解いていくことが初めは必要なのですが、読み解いた後にそのまま次に進むのではなく、 答えを隠して自らの手で解答を導き出すことが必須です。

ですから、説明事項を読み理解し、例題を読み解く。その後に例題の答えを隠して自らの手で解き直す。 これが教科書の使い方です。

教科書理解の方法

地方私立高校⇒東大理三現役合格講師 江尻（センター試験868/900）

高校数学の基礎レベルを身につけるのにするべきことは、教科書（またはそれ相当の内容をもったもの） の理解と基礎問題集の習得です。

まず、教科書の理解についてです。 効率的に内容を理解するためには、教科書の記述をしっかり最初から追うのが１番です。 「何が定義されたのか」「道具をどのように使うのか」「どのような定理なのか」 「定理を使ってどのような問題が解けるのか」などを１つずつ理解していってください。

その際、定理の証明は複雑そうだったら飛ばしてもいいと思います。 （理解レベルが上がってから立ち戻ればいいので。） ところどころにある例題もしっかり理解しながら進んでいきましょう。 そして、練習問題も自分で手を動かして解いてみましょう。 このように進めて１つの章が終わったら、 章末問題はやらなくていいのでもう１回どういう話があったのかざっと見直してみてください。

その後に基礎問題集の対応する範囲を進めていきます。 ただし、１つの章を学習しただけでも疑問はいくつか湧いてくると思うので、 次の問題集に進む前に先生なり数学が得意な人なりに質問して解消するようにしてください。 最初に間違った方向で理解したものを矯正するには、最初に学んだ時以上の労力が必要になりますからね。

基礎習得段階のインプット時の注意点

地方公立高校⇒東大理三現役合格講師 安藤（センター試験877/900）

数学はインプットし終えた段階とアウトプットできるようになる段階のギャップが大きい科目です。 その差を問題演習によって埋めていくことになります。 数学の点数はこの演習の量で決まると思います。現浪で差が大きくつきやすいのもそのためでしょう。 そのため、（基礎段階では）なるべく早くインプットを終わらせ、 （標準問題演習レベルでの）アウトプットの練習量をなるべく多く確保することが重要だと思います。

インプットのときの注意点としては以下の2点が重要です。

よくわからない点に拘泥しない

この時点で考え込むのは非常に効率が悪いです。 よく分かっている人に聞くか放置して次に進みましょう。

基礎のインプット段階でもアウトプットを適宜挟む

この段階でも問題演習を適宜挟むことです。 ここの問題は簡単なものでOKです。

概念や公式は初習の段階では完全理解は不要

地方公立高校⇒東大理三現役合格講師 安藤（センター試験877/900）

数学の教科書レベルの学習では、なるべく時間をかけず問題を多く解き、 理解度はあまり心配しないのがいいと思います。

まず、数学で習う概念や公式を理解するには問題を多く解いてその概念や公式を使う機会を多く持つ必要があります。 そのため、問題をこなす以前の段階で時間をかけて理解しようとするのは （入試で点を取るという観点では）非効率的だと思います。 ですので、初習の際は完全理解は目指さず、各公式の使い方を覚えるような形で進めていくのがいいでしょう。 そして演習を通して公式に慣れましょう。 答えはすぐに見ていいと思います。

ある程度問題が解けるようになり概念や公式に親しんだら次の問題集に移っていいでしょう。 このレベルの問題集は早く卒業して次の標準レベルの問題集（青チャート、Focus Goldなど） で時間をかけるべきだと思います。（この理由は先ほどの「基礎習得段階のインプット時の注意点」に書いてある通りです）

ここまでのお話の注意点！

以上の江尻、安藤の話の中で、
江尻が「定理の証明は複雑そうだったら飛ばしてもいいと思います。 （理解レベルが上がってから立ち戻ればいいので。）」、
安藤が「数学の教科書レベルの学習では、なるべく時間をかけず問題を多く解き、理解度はあまり心配しないのがいいと思います。」
と言っていますが、これには以下でご説明していく内容が前提となっていることを誤解しないでくださいね

簡潔に結論だけお伝えしておくと、次のレベル・段階の問題演習の過程で適宜、理解が曖昧・不十分な部分に立ち返り 確認を行っていく、理解をしていくということが前提となっています。

これは裏を返すとどいうことかというと、教科書（もしくはそれに代わる参考書）について 、東大理三に合格した彼らでも最初からすべてを理解していくことは不可能・非効率ということを意味しています。

要するに基礎をしっかり理解するというのはそれだけ難しいということであるとともに、 全体を学ぶ中で立ち返る方が本質的な理解という点でも、効率という点でも優れている部分があるということです。

【動画で解説】初習の問題集の独学の方法

当然のことですが、初学の段階で絶対に理解していかなくてはならないという部分はあります。 自分で勉強を進めていく際に、何をどこまで理解すべきで、逆にしなくていいのかの基準について 以下の動画をご覧ください。

この動画は、数学のみならず全教科を対象にお話をしていますが数学も当然前提にしています。 参考にしてください。

地方公立高校⇒東大理三現役合格講師 正門（センター試験864/900）

【動画で解説】数学の公式の理解記憶の方法

数学の基本的な公式は覚えていかなければ問題を解けません。しかし、ごくごく基本的な公式以外、 単純暗記をしていたのでは数が多く覚えにくい、複雑で数が多くなってくると混乱する、 公式の一部を忘れてしまう、等の弊害が生じます。

この弊害を除くためにはごくごく基本的な単純暗記すべき公式以外は理解暗記をしていくのがおすすめです。 実際にはこれが本質的な理解にもつながっていきます。以下ではその方法について解説します。

開成高校⇒東大理三「次席」現役合格講師 小団扇（センター試験867/900）

基礎習得のための数学問題集・参考書と勉強法

教科書及び傍用問題集

※全くの独学の場合は教科書及び傍用問題集の代わりに以下のものから入っても良い。 以下では教科書代わりの参考書を掲載する。

語りかける高校数学（ベレ出版）

「数Ⅰ編」「数Ⅱ編」と別れている。 授業のように先生が語り掛けてくる構成。 ０から始めるのであればお勧めできる。

問題数が少なめではあるが、簡単な問題を細かい段階に分けて説明してくれているので 論理の理解とともに計算力アップも図れる。

スバラシク面白いと評判の初めから始める数学（マセマ）

「数学Ⅰ」「数学A」「数学Ⅱ」「数学B」「数学ⅢPART1」「数学ⅢPART2」と別れている。 上記「語りかける高校数学」と同じく授業のような構成。０から始める人向け。これも問題数は少なめ。 書店などで両者を比べ気にいった方を選べばよい。

沖田の数学をはじめからていねいにシリーズ（東進ブックス）

「ⅠA　数と式・集合と論証・2次関数編」「ⅠA　図形と軽量・図形の性質編」 「ⅠA　場合の数と確立データの分析・整数の性質編」に分かれている。

講義口調なので、実際に授業を受けているような感覚がある。 初修の人、すっかり忘れてしまっている人にオススメ。

数学の基礎レベル段階の勉強法のまとめ

以下では、標準問題集の勉強法の説明という別の次元のお話に入るので、 みなさんの頭が混乱しないようにここまでの基礎レベル段階の勉強法のポイントを一旦ここでまとめておきます。

最初に教科書やそのレベルの参考書に当たる段階では完全理解は不要

最初に教科書やそのレベルの参考書に当たる段階では完全理解は不要でとりあえずまず全体を学ぶことを優先しましょう。

このレベルの問題集（白チャートなど）は理解のために何回も繰り返す意味はない！

このレベルの問題集（白チャートなど）は定理・定義の使い⽅・基本操作を学ぶための本なので、 解法や定石を学ぶ段階の問題集と異なり、それを目的として何回も解き直す必要はありません。

要するに後述するように、このレベルの問題集や問題演習の役割は、あくまで公式や概念の使い方を学ぶための物であって、 そこから普遍的な解法の定石やエッセンスを学ぶものではない、そのような性質の問題集ではない、ということです。

基礎が大事であることと、この段階で基礎を完全理解することは別の話です。 問題集は解法が瞬時に浮かぶまで何度も繰り返し解くというのはこのレベルの問題集には的外れな話なのです。 あくまでこのレベルの問題集は、数学の基本操作を身に着けるためのものであって理解とかとは別次元の話です。 このことはしっかり理解しておいてください。

この部分を一緒くたにしてしまっている数学の勉強法というものが巷にはありますが、 それでは数学の実力は効率的についていかないどころか実力はついていきません。 無駄な単純暗記をさせられているにすぎないのです。 数学はお経ではないのでいくら唱えようが実力はつきません。 みなさんはこの部分間違えないようにしてください。

標準問題集レベルの数学勉強法

標準問題集レベルの数学の勉強法には世間一般では明確に区別されていませんが、 実は2つの次元があります。

この2つの次元をわかっていないと、このレベルの勉強法を混同したり誤解したりしてしまいます。 世の中の数学の勉強法はほぼすべてこの部分を混同しています。

この2つの次元の違いから導かれることは、次元ごとに問題集に取り組む目的や 問題集自体の位置づけ、使い方も異なってくるということです。

簡潔に説明すると、

この「解法パータン・定石をストックする次元」と「思考力を鍛える次元」のお話の部分は 当塾のオリジナル理論である 「試験問題の3類型」「難問の2分類」「一般化脳理論」「得点脳理論」として当塾の著書、
「受験の叡智」【受験戦略・勉強法の体系書】
「医学部」受験の叡智【受験戦略・勉強法の体系書】
詳細に説明していますので、数学を得意科目にしたい方、 数学を勉強しているのに成績が伸びない方は是が非でもご覧ください。

以下では、この点も踏まえ、次元ごとに説明をしていきます。

実力が伸びない人に共通する数学対策

この段階では、先ほど述べたように解法や定石を他の問題にも使えるように一般化して理解・整理・ストックしていくことが問題演習の主目的です。 この観点から、当塾東大理三合格講師陣の書下ろし記事をご覧ください。

あなたは大丈夫？数学の試験問題の捉え方

医学部や難関理系を目指す受験生に特に多い誤りの思考過程を以下に示します。 実力が伸びない受験生には、共通する2つのパターンがあります。 皆さんは大丈夫かチェックしてくださいね。

パターン1

「入試が難関である」
→「数学で高得点をとれば有利」 →「難しい問題を出来きるようになれば差をつけることが出来る」 →「レベルの高い問題集を出来るようにしよう」 ⇒基礎標準問題集をないがしろにする。

パターン2

「基礎が大事である」 →基礎レベルの問題集を完全に暗記したり理解するまで何度もやらされている ⇒それが完璧になるまで次の問題集や参考書に移らない

勉強しても数学の実力が伸びない受験生はほぼこのどちらかで数学の勉強を考えてしまっているか、 誤解のもとに生まれた勉強法に踊らされています。

パターン２が誤りであることは基礎習得レベルの勉強法で述べてきた通りです。 以下では、パターン1の誤解について木っ端みじんに打ち砕きます。

合格の天使のオリジナルロジック「試験問題の3類型」理論を公開！

当塾の著書、
「受験の叡智」【受験戦略・勉強法の体系書】
「医学部」受験の叡智【受験戦略・勉強法の体系書】
に掲載している当塾のオリジナル理論である
「試験問題の3類型」「難問の2分類」「一般化脳理論」「得点脳理論」
について特別公開します。

言うまでもないことですが、これは当塾のオリジナル理論で著書内容の核心に関連するバリバリの著作権保護内容です。 指導関係者の無断使用・無断引用・剽窃を固く禁じます。

以上を前提に、以下をじっくり読んでいってください。お伝えしている本質を掴んでいただくことが出来ると思います。

なお、ここでは簡潔な説明にとどめましたが、当塾のオリジナル理論である「試験問題の3類型」「難問の2分類」「一般化脳理論」「得点脳理論」は数学のみならず 理科や他の教科を効率的かつ確実にマスターするために必須となる秘策です。

何が何でも難関大学や医学部に合格したい受験生や高校生の皆さんは、上記オリジナル理論と 圧倒的受験結果に実証された受験戦略・勉強法を網羅的に掲載した

「受験の叡智」【受験戦略・勉強法の体系書】▶
「医学部」受験の叡智【受験戦略・勉強法の体系書】▶

を是非手に入れてください。損はさせません。

数学の解法パターン・定石ストックのための勉強法

この段階では、先ほど述べたように解法や定石を他の問題にも使えるように一般化して理解・整理・ストックしていくことが問題演習の主目的です。 この観点から、当塾東大理三合格講師陣の書下ろし記事をご覧ください。

標準レベルの問題演習の2つの目標

地方公立高校⇒東大理三現役合格講師 安藤（センター試験877/900）

標準レベルの問題集では次の2点が目標になると思います。

●教科書〜基礎レベル範囲事項の理解を深めることと
●新しく習う解法のインプット

です。

標準レベル問題集を進めている段階で基礎レベルの理解が不十分に感じるのは自然だと思うので、 そういう時は不安に思わず適宜教科書などに戻って確認するといいでしょう。

ここでは腰を据えて理屈を考えていいと思いますが、あまり問題から離れて考えすぎるのは効率の面ではよくないと思います。 解法の理解のためという目的意識を持って行うといいと思います。

解法のインプットでは回数が重要だと思います。この学習は型を覚えるような立ち位置にあります。ここでは解法を覚えるというより身につけるような気持ちで取り組むべきだと思います。ここでの解法や発想は解答のベースとなるもので、このレベルの解法が自然に想起されるようになることが、次以降のステップで重要になると思います。だから繰り返し解いて体で覚えるべきだと思うのです。時間が十分にあるならどの問題も3〜4回は解くといいと思います。

問題演習のやり方

地方公立高校⇒東大理三現役合格講師 花村（センター試験851/900）

数学を勉強するときは5分くらい自分で考えてみますが、大抵はすぐに答えを見ます。 模範解答の考え方が理解出来たら、その解き方が自分にとって常識になるまで繰り返し問題を解きます。 ここで大切なのは問題を丸暗記するのではなく、解法の流れをイメージとして掴むことです。 それには自分でヒントを見ずに答案や計算を再現する訓練が一番いいと思います。 自分の手で書くことで単純に記憶が定着しやすくなるし、良く分かっていないポイントが見つかったり計算練習になったりと為になることがたくさんあります。この方法では所詮、自分の見たことがある、または似ている問題しか解けるようになりません。高校からこの勉強法を始めて最終的には東大数学では半分くらい解ける程度でしたが、慶應やその他の大学の問題は特に対策しなくても完答できるようになりました。僕の方法は受験数学の邪道かもしれませんが、勉強量と学力が比例して伸びていくので、時間と努力に余裕のある人にはお勧めです。もちろん初めて見た問題を一から考えて解く方が学力が付きそうですが、自分の頭脳では大変だったし、例えできたとしても時間が圧倒的に足りなかったです。教材についてはチャート式やFOCUSGOLD、大学への数学などの解説が詳しくて見やすいレイアウトの参考書がお勧めです。４STEPは解説が少ないし、 共通テスト(従来のセンター試験)の過去問は自分の手で解法を再現して定着させる作業ができないので適していません。

数学の問題集の反復の目的

地方公立高校⇒東大理三現役合格講師 花村（センター試験851/900）

理解した事項が自分にとって常識になるまで短期間に反復学習を徹底的に行います。 ここで大事なことは参考書の丸暗記をするのではなく、 問題を解くときの考え方や発想を身に付けることです。

基本事項を常識になるまできっちりと身に付けると、それ以降の学習効率が圧倒的に上がります。 難しい参考書を解いても、前の参考書に戻って復習する必要はないし、 純粋に新しい概念に集中できるからです。

問題演習から得るべきもの

地方私立高校⇒東大理三現役合格講師 江尻（センター試験868/900）

チャート式やFocus Goldなどの問題集は、 例題とそれに対応する練習問題が同じページに載っているものが多いです。 まずは例題を見て、解けそうなら自分なりにやってみて、 できてもできなくても解答解説を読んで解答の流れを習得しましょう。

問題のなかのどこに注目してどういう流れで答えに持っていこうとしているのかを読み取るようにしてください。 「これを求めたいからこの公式を使う」とか「これを求めることでこういう方向に持っていきたい」 とかを掴むようにすると良いと思います。解説の前に「ポイント」とか「考え方」とかの項目があったら、 そこを見て解答の流れを掴むヒントにしてください。

ここで疑問が生じた場合も、練習問題には進まずに、 ちゃんと理解している人に質問したほうが効率がいいです。 このようなプロセスで１問１問進めていってください。 練習問題をやるのは自分に合ったタイミングでいいと思います。

また教科書の章末問題は、ある程度基礎問題集を進めてから見てあげるといいです。 １度にすべての問題の解法を習得するのは不可能なので、 だいたいの問題が自力で解けるようになるまで復習を加えましょう。

解き方を身に着けることが主目的

地方私立高校⇒東大理三現役合格講師 佐々木（センター試験801/900）

数学は問題を解くにあたって他教科よりも思考力が問われる科目です。 その思考力というのは今までに記憶されてきた基本的な問題の解き方が土台となっていることが多く、 そのため数学力というのは練習量にある程度依存します。

まずは青チャートのような基本問題が集められた問題集を解いて、 全ての問題がしっかりと解けるぐらいまで繰り返すことが大切です。

この段階では、考える練習というよりはむしろ解き方を身につけることがメインで、 基本問題であれば問題を見てすぐに解き方が思い浮かぶぐらいにするのが理想的です。 問題を解いていくうちに公式なども自然と身についていくと思います。

【動画で解説】数学の実力を確実にあげる問題演習法

みなさんは実際に数学の問題演習をする際にどのようにノートに書いて解いていますか？ 同じ問題集をやっていてもこの解き方ひとつとっても大きな差がついているのです。

数学の実力差を分けているのは、出来る人がやっているちょっとしたコツや当たり前の思考の集積の差でもあるのです。 以下の東大理三合格講師正門の動画でその一端を公開します。 自分の数学の問題集の取り組み方を検証しなおしてみてください。

地方公立高校⇒東大理三現役合格講師 正門（センター試験864/900）

このの動画の内容は、数学の問題演習を行う過程の一部にすぎません。 問題演習を行う際のチェックポイントは他にもいくつかあります。 復習方法も含めればさらにポイントは増えます。

大事なことは、こういったちょっとしたコツや実践方法の差が、 数学の実力差につながっているということです。

当塾の受講生はこういった点も含め、数学に限らず、全教科について、最も優れたものを有している東大理三合格講師陣からすべてを手に入れることが出来ますが、みなさんもひとつづつ実践していってみてください。どの教科であっても、得意科目にすることが可能になります。 しっかり実践して、数学の実力を確実に高め、それぞれの第一志望合格に向かってください。

このレベルの標準問題集の裏話

上記で、当塾の東大理三合格講師陣のアドバイスを掲載していますが、黄チャート・FocusGold・青チャート等については、 標準問題集という位置づけではなく「基礎問題集」という位置づけで原稿を書いてくれた講師もたくさんいます。

これは、彼らのレベルが高いからということでは決してありません。この部分の冒頭で述べた話を思い出してください。 解法パターン・定石ストックの次元での標準問題集の捉え方として「基礎問題集」と彼らがとらえているのは、 ここまでが数学の問題を解くための下準備という意識がしっかりしているからです。

決して内容が簡単であるから「基礎」ととらえているのではありません。実際に彼らも青チャートなどを最初に解いた時 全くできなかった、というのが現実なのです。

ただし、本番の入試問題を解くにはまずこの次元の問題集をマスターしなければならない、という強い意識があったのです。 だから、意識付けとしてこの次元での標準問題集は「基礎問題集」としてとらえているのです。

できない=才能がないのではなく、出来なくても出来るようにしなければ始まらない、という意識を皆さんも持ってしっかり取り組んでください。

解法パターン・定石ストックのための問題集

基礎～標準問題集
　 ※基本的には志望校の数学の問題の難易度に合わせ、以下のうちから 一冊をまず完璧にし、 その後、志望校の過去問を解いてみてほしい。 数学の入試問題として「第2類型難問題」（当社、合格の天使オリジナルロジック）が主である大学（旧帝大理系等）以外は、 このレベルの問題集一冊を完璧にして志望校の過去問演習を行えば十分 な得点を獲得できる。

『黄チャート』（数研出版）

「数学Ⅰ+A」「数学Ⅱ＋B」「数学Ⅲ」と別れている。 網羅性はかなり高い。この問題があらかた解けるようになったら、 数学の難度が高くない大学であれば、高得点が期待できる。

ただ、解法に 対する問題数が少ないので、志望校の過去問演習を行い、 重要な部分は 必要と感じれば他の問題集の問題も活用するとよい。

※志望校の数学の問題の難度や得点戦略によっては このレベルの問題集で足りることもあるので各自の志望校の問題の難度は チェックできる人にチェックしてもらうことを勧める。

『Focus Gold』（啓林館）

基礎～標準レベルを中心に幅広く出題パターンを網羅していて、 掲載 問題数が多く難易度の幅も広い問題集である（解答、解説は一対一と比 べると劣る印象がある）。 巻末に入試問題を題材とした発展的研究事項 が記述されており、面白くためになるのだが、 体裁に気を使っておらず ただ事項を書き連ねたようになっていて見づらいのが難点。 初修で基礎を網羅するために、解説を隠して例題だけ解けば十分。 標準～の問題は １対１など他の参考書を使ってもよい。

『青チャート』（数研出版）

「数学Ⅰ+A」「数学Ⅱ＋B」「数学Ⅲ」と別れている。 標準問題集。問題数がかなり多いが網羅性が高い。 計算量もそれなり に多く、難しい問題も含まれている。 志望校の数学の問題の難度によっては黄色チャートやFocus Goldで十分な場合があることに注意。

『１対１対応の演習』（東京出版）

「数学Ⅰ」「数学A」「数学Ⅱ」「数学B」「数学Ⅲ微積分編」「数学Ⅲ曲線・複素数編」と別れている。 大学入試における典型問題を集めた網羅型問題集。 Focus Goldや青 チャートと異なり教科書レベルの問題はほとんどない。

特長としては、 扱っている解法自体がかなり洗練されており、 またその解法を選択する 理由を平易な問題を題材にうまく一般化して解説している。 このため掲載している問題数は多くないのだがカバーできる問題範囲は広い。

数学的思考力養成のための勉強法

この段階は志望校や現状に応じてやらなくてもいい人がほとんどです。この点注意をしてください。 以下では、この点も含め解説していきます。

多くの受験生はこの段階は飛ばし過去問演習へ移ってください

この部分は、東大や旧帝大の医学部や理系学部や東工大などの数学に思考力が必要となる数学が出題がされる大学の受験生で、 かつ、時間的に余裕があって、さらに他の科目との勘案や得点戦略上数学で高得点を獲得する必要がある受験生のみが対象だと考えてください。 （また、これらに当てはまる受験生であっても、まずは解法パターン・定石ストックのための標準問題集のマスターが最優先であることは肝に銘じてください）

地方国公立医学部や一般的な難関理系であれば、解法パターン・定石ストックのための標準問題集の次元を終えたら志望校の過去問演習に移り、 過去問でその使いこなしやアウトプット力を万全にしていってください。これが最も効率よく合格点を獲得する方法です。

地方国公立医学部や理系・文系の場合には、高度な思考力が要求される問題は出題されません。 解法パターン・定石ストックのための標準問題集でしっかり解法や定石を他の問題にも使えるように一般化して理解・整理・ストックし、 過去問演習で使いこなしを鍛えておけば対応できます。

この部分を誤解してしまう受験生が多いですので、当塾の著書、
「受験の叡智」【受験戦略・勉強法の体系書】
「医学部」受験の叡智【受験戦略・勉強法の体系書】
に「一般化脳理論」「得点脳理論」「過去問至上主義」というオリジナル理論を詳細に説明していますので、 不安がある方は是非ご覧ください。

過去問演習のやり方については、このページ内で説明していますので、 この部分を飛ばし過去問演習の部分をご覧ください。

思考力養成のための問題集の進め方

地方私立高校⇒東大理三現役合格講師 江尻（センター試験868/900）

進め方は基礎標準問題集の進め方とほとんど同じで大丈夫ですが、 このレベルの問題集の場合に注意するべき点を挙げたいと思います。

まず、問題の内容（レベル）が入試レベルに近づくので、 解法が複雑なステップを踏む問題が増えてくるということです。 なので、より注意深く解答を読み込む必要があり、 自分で解答を構築するにはどこに取っ掛かりを見つけたら良いのか、 どういう発想をストックしておかなければいけないのか、 ということを基礎レベル以上に考えていく必要があります。

１周目では理解に重点を置き、
２周目以降では記述解答の構築に重点を置く
と良いと思います。

具体的には、例えば場合分けが必要な問題で、 自分で解くときに場合分けがちゃんとできるためには、 解法を理解する時点で「なぜ場合分けが発生するか」 「どのタイミングで気づくのか」などということまで頭が回っていた方がいいですよね。

また、解法の要素自体は基礎レベルのものとオーバーラップする部分が多いはずなので、 解法の中で自分の理解が怪しいと思ったステップは基礎問題集に戻って確認・演習する必要がありますし、 自分で正確にできる自信がない計算に遭遇した場合は基礎問題集や計算問題集などである程度自信がつくまで 同じ形式の計算をやりこんでみたりするといいと思います。 どの教科でもそうですが、少しでも気になるなぁと思うところがあれば、 放置せずにすぐに基礎に立ち戻って確認するということが重要です。

問題演習のポイント

地方私立高校⇒東大理三現役合格講師 岡元（センター試験873/900）

数学の基本的な典型パターン問題ができるようになったあとは、難しめの問題集を勉強します。 大事になってくるのは、1回目に解くときはなるべく粘って考えて慎重に答えを出し切ろうとすることです。

すぐに答えを見たり計算を諦めたりする癖をつけると、 入学試験の時にも初見の問題にうまく対応できなくなってしまうかもしれません。 できなかった問題も何度か復習してしっかり解けるようにします。

様々なアプローチを駆使する

地方私立高校⇒東大理三現役合格講師 佐々木（センター試験801/900）

基本的な解き方がある程度身についてからは、 より応用的な問題や初見の問題を解いていくことになると思います。 その際大切なことは、分からない問題に出会ってもすぐに答えを見ずに、 じっくりと考えることです。

本番は制限時間内に解くことが重要ですが、その練習をするのは二の次です。 ゴリ押しでもなんでも良いので様々なアプローチを駆使して、 問題をなんとかして解こうとする姿勢で挑むことが大切だと思います。

それでも解けない場合は解答を見ても良いですが、そのとき注意することとして、 ただ解法を見て納得するのではなく、 本番でこの問題を見たときにどのようにしてこの解法に至ることができるのか、 というのを意識することが大切です。

たまに見たこともない解法や思いつくのが非常に困難な解法があると思いますが、 その場合は素直に解き方をストックするのが良いでしょう。 十分時間をかけて考えた分、印象にも残りやすいと思います。

数学的思考力養成のための問題集

このレベルの問題集をやろうとしている人であっても、志望校の過去問が第一優先順位です。 まず志望校の過去問を数年分解いてみて目標点まで解けるならこの段階の問題集を挟む必要はありません。 初見の問題に対する視点や思考を鈍らせないようにするために適宜このレベルの問題集の問題をや ってみるという使い方はありです。

１．志望校の数学の問題が思考力を要求されるものであるという客観的事実があり
２．かつ、各自の得点戦略上この段階の問題集を挟む必要があり、
３．かつ時間的に余裕がある
という条件を満たす場合にのみ、この次元の問題集は使用してください。

使用する場合の選別の基準としては、各自が「解法パターン・定石ストックのために利用した問題集」よりも 一段上のレベルの問題集を使用します。

解法パターン・定石ストックのための問題集で、 青チャートやFocusGoldを使っていた人は「1対1対応の演習」を用いればよいです。

※以下は、数学の試験問題が「第2類型難問題」（当社、合格の天使オリジナル理論）のみで構成される大学を受験する場合以外は ほとんど必要がないことに注意していただきたい。

『新数学演習』（東京出版）

大数B～C（標準～やや難）の難易度をメインに、 よく出題される問 題を分野ごとにまとめた問題集。 難易度が過大評価されがちだが第２類系難問題の最も上位の難問題と言える問題（大数D評価）は5％程度。 巧みな解法が多くのっていることが特長の一つである。解説はあっさり しているため『1対1』にあるような解法はきちんと理解している必要 があるだろう。

『マスター・オブ・整数』（ 東京出版）

受験生にとって対策の難しいことで知られる整数問題に絞った問題集。 基本レベルの問題から大学受験レベルを超えた問題まで網羅されて いるので、 この本を一冊やりこむだけで整数問題対策は充分であると言 える。 本書は全部の問題をこなすには難しすぎるが、 どのように進める べきかが読者のレベルごとに書かれているので それを参考にして取捨選 択をしながら学習すれば問題ない。 東大などの、難しい整数問題が頻繁に出題される大学を目指すのであれば役に立つだろう。

『マスター・オブ・場合の数・確率』（東京出版）

上の問題集と同シリーズの、場合の数・確率バージョン。 場合の数や確率は頻出だが、この問題集が解けるようになれば、 ほとんどの問題は 解けるようになったといってよい。 『マスター・オブ』シリーズは自身 の学習状況と志望校の出題状況をふまえ、 必要かつ（時間内に）実行可能と思ったらやるといいだろう。

『月刊大学への数学』（東京出版）

受験数学誌。問題集としては、月ごとに決められたテーマ（確率、III 積分など） の問題を教科書～やや難まで、レベル別に分けて掲載している。 また、より狭い事項（（ex）|sin x|の積分など）を掘り下げた解説（類 題研究など） も（別立てで）掲載されている。分野に絞った対策に有用 と言えるだろう

数学の過去問演習を最大限に生かす勉強法

過去問演習には大きく2つの目的があります。

１つは「得点脳理論」として当塾の著書、
「受験の叡智」【受験戦略・勉強法の体系書】
「医学部」受験の叡智【受験戦略・勉強法の体系書】
に説明してある、「志望校特化型得点脳」を鍛えることです。

この目的は、志望校で要求されている数学の解法パターンや定石の「使いこなし」を学び、基礎標準問題集の知識を「過去問基準でとらえなおす」目的です。

もう１つは本番の予行演習としての意味です。問題の取捨選択、時間配分、とるべき問題の見極めの方法を学ぶ目的です。

以下では、この2つに分けて解説します。

数学の過去問演習　標準問題集を「過去問基準でとらえなおす」勉強法

過去問集を基礎標準問題を「過去問基準でとらえなおす」目的で使用する場合のポイントについて解説していきます。

過去問をやる順番

地方私立高校⇒東大理三現役合格講師 江尻（センター試験868/900）

標準問題集で一通り典型問題を学び終えた人向けに、志望校の過去問のやり方を説明します。 まず、やる順番ですが、直近の年を直前期のために残しておくという話はよくありますが、 これはある程度は理にかなっていると言えます。 というのも、自分の受ける年の入試に最近の傾向が反映される確率は昔の傾向が復活するよりも 確かに高いからです。

しかし数学（特に国公立大）に絞って言うと、 出やすい分野というのは確かにあるかもしれませんが、 問じ内容の問題が続いて出題されることはほとんどないと思うので、 最近のものを避けておくというのは必須ではないと個人的には考えています。

また、遡るか降りてくるかというのもセオリーはなく、自分の好きな方を選べばいいと思います。

具体的な過去問演習の方法

地方私立高校⇒東大理三現役合格講師 江尻（センター試験868/900）

具体的なやり方です。時間は直前期までは計っても計らなくてもいいと思います。 また、最初は何も見ずに自分の知っている解法などをぶつけて解いてみるべきですが、 わからなかった場合は解答を見る前に標準問題集や基礎問題集に立ち戻って ヒントを探してもいいと思います。

それでも分からなければ解答解説を見ますが、その際に、解答を追うだけでなく、 何に着目すればよかったかを反省したり、すでに学習していた発想なのかどうかを 問題集などで確認してみたりしてください。

過去問演習の意義は、数学の場合、過去問と同じ問題を解けるようになることではなく、 知っている形式の問題ではミスなく確実に解答を書けるようになること、 初見のものに対するアプローチを練習して解ける確率を上げていくことです。 ただ解答を眺めて納得することよりも、何が足りなかったのかや何を勘違いしていたのかなどを 反省することの方が大切です。

過去問演習では、採点者に伝わる記述答案を構成できるかどうかという要素も重要になります。 それまで記述答案を意識してきていない場合、すぐにうまく書けるようになるわけではないので、 標準問題集の復習などの際にはどういう風に記述しようか（順番、場合分け、図など） と考える習慣をだんだんつけていくとといいと思います。

本番の予行演習としての過去問演習の方法

本番の予行演習として、問題の取捨選択、時間配分、 とるべき問題の見極めの方法を学ぶ目的で過去問演習をする場合のポイントについて解説します。

究極のアウトプット＝過去問演習

地方私立高校⇒東大理三現役合格講師 深川（センター試験869/900）

数学の過去問演習は今までの問題集で得た知識と経験をフルに活用して問題を解いていく作業です。 究極のアウトプットと言えるでしょう。

問題の解き方や復習の仕方は標準問題集を解くときと変わりません。 ただ、必ず時間を計って解くようにしましょう。時間制限の中で入試問題を解くというのが大変なのです。

また、入試問題は全ての問題が解けないと合格しないというものではありません。 問題の取捨選択の仕方も過去問演習を通じて学んでいく必要があるのです。 ですから、必ず時間を計って時間内に得点を最大にするような戦略を立てていきましょう。

確実に自分が解ける問題から解答していきましょう。 今までに見たことのないような問題が出題されても、 すぐに諦めるのではなく取っ掛かりを探してみましょう。 例えば抽象的な問題であれば具体化してみましょう。 数式をおいてみましょう。また、実験をしましょう。 数が大きいときや一般的なnについて求める問題などは、 まずは小さい数字を当てはめて規則性を探してみるなどは良い手です。 このように手を動かして実際に試しながら問題を解いていくことをお勧めします。

問題集を解く時よりも気をつけてほしいこととしては、答案の書き方です。 答案を書く際に採点官に伝わるように論理立てて説明をしましょう。 説明がない答案は点数になりません。説明を上手にするやり方も過去問演習で学んでいくのです。 解き終わった後は自らフィードバックをしましょう。この問題はここに気づけば解けたな、 この問題はここまで解ければよかった、など作戦を立てましょう。 傾向と対策を練ることが過去問演習の意義です。

予行演習としての過去問演習で大事なこと

地方私立高校⇒東大理三現役合格講師 岡元（センター試験873/900）

基礎も固め、演習も積んだら過去問演習に入ります。 過去問演習で大切なのは、一度試験時間を測って解くことだと思います。 時間が限られている中で点数を取ることができるように何セットも解いて慣れることが必要です。 また、一度時間を測って解いたあとは、解き終えられなかった問題を少し時間をかけて考えてみたり、 できなかった問題をしっかり復習して次に似たようなものが出た時に解けるようにしたりすることが大切だと思います。

おすすめしない過去問の勉強法

都内私立高校⇒東大理三現役合格講師 佐伯（センター試験828/900）

僕が、過去問を解く際にこれはやらない方がいいだろうと思っている勉強法を2つ紹介します。

まず、時間を計らないでダラダラ解くことです。 試験本番では実力があってもプレッシャーに打ち勝てないとうまくいきません。 緊張していると時間制限が普段よりも重くのしかかって来るでしょう。 そのため、家で解く際もそれに慣れるよう意識しましょう。

もう一つは、音楽を聴きながら過去問を解くことです。 普段の勉強で集中力が切れてきた時に気分転換として音楽を聴きながら勉強するのはやっても良いと思います。 しかし、試験本番中は当然音楽なんて聞けないです。 音楽を聴かないと勉強する態勢になれないという人もいると思いますが、過去問を解く際はやめた方が良いです。

過去問攻略は、入試で合格するのに最も必要であり、近道でもあります。 一回一回の過去問を時間配分や取捨選択も含めてできるだけ本番に近づけた状態で大切に解きましょう。 特に数学については、試験戦略的な面が大事になってくるでしょう。 もちろん、分からなかったところの復習もお忘れなく。

数学の実力をあげるために必須となる記述答案対策

過去問演習の部分でも、東大理三合格講師陣がふれているように、 記述答案が必要とされる大学を受験する場合、この部分は多くの受験生が考えている以上に重要です。

「数学の問題が解けること」と「記述答案＝本番で得点が取れること」はイコールではないのです。 どんなに数学の問題で解答が導ける実力をつけようがこの部分が曖昧では合格点、高得点は取れません。

さらに、多くの受験生が気づいていないことですが、記述答案を論理的にしっかり書く、 ということは数学の実力を確実かつ効率的につけていくための秘策でもあるのです。

以下では、数学の実力をあげるために必須となる記述答案の書き方やその効用について解説していきます。

数学での記述答案の作り方

地方私立高校⇒東大理三現役合格講師 江尻（センター試験868/900）

今回は受験生が苦手にしがちな数学の記述答案について書きます。

普段の勉強では記述答案を意識しながらやることはほとんどないと思うので、 いざテストや模試になって記述形式にされた時に不適切なものを作ってしまう人が多く見受けられます。

それを防ぐために普段から答案についてよく考えてほしいのですが、 そのヒントとなるようなことをいくつか挙げてみます。

まず、答案はメモ用紙ではなく数学的論証の痕跡なので、 一貫した論理性が要求されるということです。 具体的に言うと、例えば求値問題（「?を求めよ」系の問題）なら、 その答えに至った理由を完全に説明したければなりませんし、 証明問題なら仮定からどのようにして結論に至ったのかを1点の曇りもなく記述しなければなりません。

次に、答案を評価するのは採点官で、採点官は答案からしか受験生の考えたことを分からないということです。 例えば、求値問題で値が違ったときに採点官が「分かりにくい」とか「読む気が起きない」 と思えば部分点が与えられない可能性がありうるという事です。

これを踏まえて具体的にどうすればよいのか考えると、 まずは論理的な飛躍を作らないということです。 自分では分かっていても、解答の肝となるところは省略せずに書くということです。

次に、余計な論証・計算はなるべく省こうとするということです。 解答の本筋に関係ないことや、だらだらとした計算は解答に書くと悪印象を与えてしまいますし 理想的な答案ではなくなります。 解答にはメリハリが必要で、必要なこととどうでもよいことがあります。 それを問題演習を通して吟味していくのは、答案作成を意識していないとできないことですので、 普段から模範解答や自分の答案を分析して問題の本質により迫っていくような勉強をすると良いと思います。

【動画で解説】数学の記述論述答案のポイント

ここでご紹介する動画は、数学の勉強法｜大学受験数学の勉強法まとめ ▶ のページでご紹介している動画ですが、非常に重要なことですのでこのページでもご紹介します。

数学の記述・論述答案は単に本番で得点するためだけに書くためのものではなく、 普段の勉強で数学的な論理や独特の文法を学び数学の実力をつけるためにも必要なもの なのです。

ただし、評価される数学の記述・論述答案ってどういうものなのかがわかっていなければ いくらこれを日々の数学の勉強法として実践しようとしても的確に実践できません。 そこで評価される数学の記述・論述答案について動画をプレゼントします。

この動画はこの講義を受けることで数学の実力を伸ばし旧帝大や医学部医学科へ合格している受験生から 絶賛されている「数学記述・論述講座」のイントロダクション部分の無料提供です。 是非役立ててください。

東大理二トップ合格講師 大久保（センター試験881/900）

国公立2次数学と私大数学の対策の違い

以上解説してきた数学の勉強法は、すべての受験生に有益なものですが、 志望校が国公立であるのか、私大であるのかによって重点を置くべき部分が異なります。 それぞれの問題特性を知り、効率的な対策をしていきましょう。 以下ではこの部分について解説していきます。

二次数学(国立)の特徴と対策

都内私立高校⇒東大理三「次席」現役合格講師 小団扇（センター試験867/900）

国立の二次数学はthe王道といった問題形式であることが多いです。 軌跡や確率漸化式などのごつい問題が出されがちです。 解くのに知識が必要な問題はあまり出されません。

私立と違って答案も書かせるので、減点されないような答案を書く練習も必要です。 添削を受けないとと自分で気づけない論理の漏れがあるかもしれません。 自分が落としやすい箇所(わる数≠0の確認など)を演習を通じてノートにリストアップして、 そこに書いたミスは二度としないという意識でいるといいと思います。

東大以外の大学でも、東大の出題形式に少し似せてくる場合もあるので、 東大を受けないにせよ去年分の過去問に目を通しておいてもいいかもしれません。

対策としては、奇抜なことは必要ないです。 基礎問題集で基礎を固め、標準問題集で問題の解きほぐし方や定石を学び、 過去問で実践し、その大学の傾向をつかむ　といういたってシンプルな勉強法がベストです。

問題一問一問が重く、しっかり理解しているかどうかを聞いてきているので、 基礎固めがとても重要になります。徹底的に基礎を固めましょう。

私大数学の特徴と対策

私大数学は、大学にもよりますが、クセの強い問題を出すところがあります。 めちゃくちゃ複雑な積分計算だとか、大学範囲の数学をなんとか高校数学に落とし込めたようなものや、 知識があるかないかで大きく差がついてしまうものなど、いろいろな質の問題が出されてしまいます。

また、大学によって、大問５つといったところもあれば、小問が10~20題といったところまで、 いろいろな出題形式があります。 なので、過去問のチェックや演習を通じて、その大学の特色をつかむことが非常に大事になります。

また、答えのみをマークシートに書かせる大学も多く、 そういった場合は途中式による部分点がないので、計算ミスを絶対にしないように、 慎重に計算を進めないといけません。

以上のことから、国立やセンターに比べて各大学の対策が重要になります。 過去問を大切に解きましょう。

共通テスト数学と2次数学の優先配分勉強法

共通テスト数学と2次数学ではその問題の性質に大きな違いがあります。 共通テスト数学をやっていれば2次数学が出来るようになるとか、 従来のセンター数学が2次数学の基礎であるという捉え方は明らかな誤りです。 以下では、共通テスト数学と2次数学の問題の性質について解説し、優先的な配分法を解説します。

共通テスト数学と二次数学の違い

都内私立高校⇒東大理三「次席」現役合格講師 小団扇（センター試験867/900）

共通テスト数学と二次数学にはたくさんの違いがあります。 その中でも大きなものが、出題の広さと深さです。

共通テスト数学は教科書に載っているあらゆる範囲から出題されます。 なので、網羅性は二次数学よりも広くなっていますが、 ほとんどの問題は定理を1つ使えばおしまい、というように一問ごとのウェイトが軽くなっています。 出題範囲が広く、また、様々なレベルの人が受けるため、踏み込んだ出題ではありません。 つまり、広く浅い出題といえます。

これに対し、二次数学は積分面積計算や確率漸化式など、 出題されやすい分野が存在します。 逆にデータの分析や初等幾何からは出題されにくい傾向にあります。 ただ、一問一問が重く、設定を把握し、問題文をひも解き、 知っている解法に落とし込むというように踏み込んで考える必要があります。 共通テストに比べると、狭く深い出題です。

イメージとしては、共通テストが教科書を隅から隅まできっちり読むことを要求しているのに対し、 二次は重要な部分をしっかりと深く理解することを要求しているイメージがあります。

問題の性質と志望校の配点比率から優先度を決定すべし

忘れている範囲を浮き彫りにしてその穴を埋めるのに共通テストは使えますが、 二次のような深い問題には対応できません。

従って、共通テスト対策ばかりしても二次の得点には結び付きにくいです。 逆に、二次対策をしていれば、あとは初等幾何やデータの分析といった共通テスト特有の問題の対策さえすれば、 共通テストは解けるようになります(スピードなどの問題はまだありますが)。

こういった違いを意識して、共通テストと二次どちらを先にすべきかを自分で考えてみましょう。

受験数学における計算力の重要性とその対策

冒頭で数学の実力をあげる勉強法として大きな柱が３つあります、とお伝えしました。 今まで述べてきた、「基礎の習得」「思考力の養成」と並んで数学の実力をあげるために必須となるのが 計算力・計算スピードの養成です。以下ではこの点について説明していきます。

計算力の位置づけ

地方公立高校⇒東大理三現役合格講師 安藤（センター試験877/900）

ある受験参考書（『数学の計算革命』）には以下のようなことが書かれています。 受験数学を解くのに必要な力は知識、発想力、計算力の三つであり、そしてこれらは相互に補い合うものだ。 つまり、解法を思いつく発想力が足りなくても似たような問題を解いた経験があればカバーできるし、 計算力が無くても計算がなるべく少なくなるような巧い解法を思いつく発想力があれば得点できる。

私も同意見です。計算力はしばしば基礎に位置付けられますが、 むしろ数学の得点能力を左右する最も重要な要素の一つとして、 ほかの能力と並列で考えるべきものだと思います （加えて、これらは相乗効果で伸びていくものだとも思います）。 ですから、たとえ受験終盤であっても、 計算力向上に焦点を当てた演習の時間を意識的に設ける意義は十分にあると思います。

計算力向上のメリット

地方公立高校⇒東大理三現役合格講師 安藤（センター試験877/900）

計算力が身に付くと重い数IIIの積分計算問題も安定して得点できる（むしろ得点源になる）ようになり、 全体的に数学の得点がかなり安定してきます。 特に数III分野が出やすい医科大学志望の方は意識的に強化を図ってください。

また、文系や数学が苦手なひとは 計算するだけの問題を取り切って底点を安定させる必要があるため、 正確な計算力が不可欠になります。

加えて計算練習は時間をとらず、総得点に対するコストパフォーマンスが高い演習になりますから、 数学にあまり時間を割けない人でもやる価値はあると思います。

数学の計算力を養成するための勉強法

計算直の養成として必要になるのは、「何をどうやるべきか」と「計算ミスを防ぐ方法」を確立することです。 計算ができるようになってもミスをしてしまえば計算が出来ないことと同じです。 ですので、計算ミスを軽く見ないでミスを防ぐ方法についてもしっかり対処しておきましょう。 以下ではこの点について解説していきます。

計算力を養成するためにやるべき事

地方公立高校⇒東大理三現役合格講師 安藤（センター試験877/900）

計算力は技術力と筋力のようなものに分けられると思います。 技術力とは、速い計算の仕方や考え方を使いこなす力のことです。 計算のテクニックで大したものはあまりありませんから、 少し問題を解いて慣れれば身に付きます。

他方、筋力は、計算を頭の中で処理していく力のことで、 これは負荷をかけながら毎日続けていかなければ伸びていかないと思います。

やることとしては、短い時間でいいので毎日時間をとって、 数値設定が厄介な（結果がきれいでない）計算問題を解いていきましょう。 分野の偏りが生まれにくいので市販の計算問題集を使うといいと思います。 この時に、なるべく紙に書く途中式の量を減らすと、 上で書いた筋力(処理能力)が鍛えられるでしょう。 集中度を高めるため、日付、かかった時間、正誤数を記録していくといいと思います。

計算ミスをなくす方法

以下をご覧いただくとお分かりいただけると思うのですが、 当塾、東大理三合格講師陣もみな計算ミスを防ぐ、 なくす方法について受験生時代非常に意識を置いていました。

このことからわかるように、数学できっちり得点するためには計算ミスをなくすことが非常に重要であり、 裏を返すと、この部分の意識が薄く、ミスだからいいや・問題は解けるからいいや、で片付けている人は 数学の実力が伸びない、本番で得点をきっちりとれないことを意味します。

数学においてはそれだけ計算が重要である、ということです。以下の体験談を読み意識的に対策をしていってください。

地方私立高校⇒東大理三現役合格講師 江尻（センター試験868/900）

計算ミスは誰でもしてしまうものです。どんなにコンピュータのような頭脳の持ち主でも、 計算問題を一万問解かされれば一問は間違えてしまう事でしょう。 なので「計算ミスをなくす」と言うのは簡単ですが、実際にはできることではなく、 大切なのは「いくつかの方略をたてて計算ミスをする確率を限りなく減らしていくこと」です。

計算ミスを減らすためには、まず丁寧に式変形をする習慣をつけることが大切です。 しかしこれは「できるだけ間の式をたくさん書け」ということではありません。 展開をいちいちしたり代入を数段階に分けてするのは写し間違いの確率を高めます。「

丁寧に」というのは、些末な計算はできるだけ頭の中でやって大事なところは丁寧に書いて間違えないようにするということです。 （ただし、どこまでを頭の中でやれるかはどれだけ計算をしてきたかに大きく依存するので慣れの範疇に入ってきます。）

次に、自分のしやすいミスをミスするたびに分析するという事です。 入試に使われる計算の種類はたかが知れているので、注意しながら問題演習をしていれば 自分が間違えやすい計算や状況が見えてくるはずです。

また、計算をし終わった後に大切なのは検算をすることです。 検算は色々やりかたがあるのでそこはまた機会があれば書こうと思います。 計算は筋トレのようなものなので、面倒くさくても「早く正確に」を目指してモリモリやってみてください。

地方公立高校⇒東大理三現役合格講師 花村（センター試験851/900）

こんにちは、講師の花村です。

ぼくは計算ミスをなくすために、ノートや答案で文字を見やすく書いていました。 その為に気を付けるべきポイントは三つです。 丁寧な文字を書くこと、文字の間のスペースを十分にとること、文字は大きく書くことです。

はじめはノートを使うときにもったいなくて、狭いスペースに小さい字で詰め込んでいたのですが、 見間違いからの計算ミスが非常に多くて大変でした。

しかし、スペースを大胆に使って文字を書くようになって、文字の書き写しの計算ミスが減ったり、 答案を書いている時のストレスが大幅に軽減されて単純な作業ミスも減りました。

僕の方法では、ノートのページを大量に消費していきます。 なんだかもったいないような気もしますが、そうはいってもノートは安く手に入るし、 その程度の投資で計算ミスが減って点数が上がるのならばむしろ安いものかなと思います。

地方私立高校⇒東大理三現役合格講師 深川（センター試験869/900）

こんにちは。講師の深川です。

数学において、計算というのは非常に重要です。解き方がわかっていても、 計算を間違えてしまうと減点されてしまいます。 また計算が遅いと数学の問題を解く時間が長くなり、 数学の問題を解くモチベーションも下がってしまいます。

数学の計算ミスというのはある意味避けられないものです。 一つも計算ミスをせずに問題を解けることは稀でしょう。 ですから、計算ミスを減らすには見直しが大切になってきます。

見直しも、すべての問題が終わってからするだけでなく、 ひとつの式変形をした後に見直すことも大切です。 自分が普段間違えやすい式変形を分析して、 その変形の際に細心の注意を払うなどの工夫をしてみると、 計算ミスは減らせますよ。

地方公立高校⇒東大理三現役合格講師 安藤（センター試験877/900）

こんにちは。安藤です。

私は計算ミスが非常に多く、苦労していました。 ですが対策としてノートにミスした箇所を逐一記録するようにしたところ、最終的にかなり改善しました。

まず、記録しようとするとミスの内容をきちんと把握することが出来ます。 これによりどういう状況で起こったのか、原因は何なのかといった分析につなげていくことができます。 このとき、なるべく丁寧に状況を見ていくことで、自分の犯しやすいミスの種類がわかってくるでしょう。

例えば私は符号ミスが多かったのですが、記録していった結果、特にカッコの外についている マイナスの符号を見落としやすいという事がわかりました。 これによって、試験場でその形が出てきたら印をつけ、 見直しの際特に注意するなどの対策を立てることができ、同種のミスを減らすことが出来ました。

丁寧に記録し細かく分析することで効果的にミスを減らしていくことが出来ると思います。 なお、この記録は計算ミス以外の間違いについても行っていました（毎回ではありませんでしたが）。 ミスを性格の問題にしてしまうと思考がストップしてしまいやすいので避けるべきだと思います。

都内私立高校⇒東大理三「次席」現役合格講師 小団扇（センター試験867/900）

こんにちは、講師の小団扇です。

問題を正解するうえで、大きな壁となるもののひとつに計算ミスがあります。 計算ミスをしてしまっては、方針はあっていたとしても大きく減点されてしまいます。 計算ミスを減らす工夫は必要不可欠です。

僕の場合は、計算スピードは自信があったのですが、 正確さに難があったので、ゆっくりと計算して答えを合わせるよりも、さっさと計算をして、 こまめに検算するという、質より量を重視した解き方をしていました。

スピードより正確さに自信がある人は、 逆にゆっくりと計算して一回で合わせるようにした方が効率がいいと思います。

他にも、割り算は最後に一気にまとめる、とか、単位の検算をする、 とかいろいろなテクニックがあります。 問題を解いていくうえで色々な解き方を試してみて、自分に合ったものを見つけましょう。

計算スピードを上げるための勉強法

計算ミスをなくし計算力をつけても、計算スピードがなければ、制限時間が課される受験では、計算力はないも同じです。 以下では計算スピードを上げるための勉強法について解説します。

地方公立高校⇒東大理三現役合格講師 花村（センター試験851/900）

計算ミスをなくすことは大事ですが、それと同じくらい重要なのは計算の速さです。 最終的には速く正確に計算することが必要になります 。正確性は短期間に上げられる一方で、 計算速度は継続して練習しないとなかなか向上しないと僕は思います。

また、高速で正確に計算できる人がゆっくりと正しく計算できることは自明ですが、 その逆は真ならずだと思います。 入試までまだ時間がある人はまず、計算速度を上げるように訓練をした方がいいです。 そのうえで、入試が近づいてきたら正確に計算をできるように徐々に慣れていけばいいと思います。 もちろん、余裕のある人は両方とも並行して訓練できれば最高です。

計算力/計算スピード養成のための問題集・参考書

以上述べてきたように、計算力や計算スピードというのは数学の実力をあげるために重要なものです。ですので、計算に特化した問題集を使うこともおすすめです。

青チャートなど計算問題もたくさん載っている問題集を使う場合には、計算力・計算スピードを養成する問題集を別途使う必要はない人もいますが、そのような問題集の単純な計算問題の部分と理解の部分を分けて、計算力は以下の問題集で鍛えるという方法もありです。

計算量が多い数Ⅲなどを苦手としている人は数Ⅲだけ使ってみるという手もありです。

『数学の計算革命』（駿台文庫）

上手い人の計算の仕方を真似させようという発想のもと、入試でよく 使う計算に絞って処理の仕方を教えている。

特徴的な方針として、紙に 書くメモ（途中計算）の量をなるべく減らす練習をさせている。

『合格る計算』（文英堂）

「数学Ⅰ・A・Ⅱ・B」と「数学Ⅲ」の2冊に分かれている。

計算力を付けるための問題集。定積分や三角関数の合成といった、基本的な手法の問題が1トピックにつき何題も掲載されている。計算の テクニックも実践的なものが紹介されているので、実際の問題を解くう えで非常に役立つ。練習問題の最後のほうの問題は難易度が高めなので、 そこは飛ばしても構わない。

数学の実力が上がらない時にチェックすべき勉強法の5つのポイント

数学の勉強をしていて実力が上がらない、初見の問題が解けない時には、 以上の勉強法を逆からさかのぼって考えてみることが大事です。

それぞれの基礎、標準、過去問それぞれのレベル・次元において、
「やるべきことをやっているか」
「正しいやり方でやっているか」
「間違った勉強法をとらされていないか」
「無駄なことをやっていないか」
について上記をしっかり読みなおしてチェックしてみてください。

知識・思考習得部分における具体的チェックポイント

解けなかった問題については、とりあえず、
１、解くための基礎を覚えていない
２、解くための基礎を理解していない
３、基礎の運用方法に気づかない
の3パターンに分けて考えてみてください。

計算部分における具体的チェックポイント

問題が解けなかった、時間内に解けなかったという場合は、以下も併せて検証を加えることが必要です。
１．計算力（そもそも前提の計算が間違っていれば、解法を学ぶという問題演習の段階に達しません）
２．計算スピード（時間内に問題が解き終わらないのは、 そもそも、どの手を打つべきかの定石自体が浮かばない事の他に計算スピードが遅いことも要因です。 このどちらに原因があるのかを分析することは非常に大事です。）

現状に余裕がある高校1、2年生の数学勉強法

地方公立高校⇒東大理三現役合格講師 正門（センター試験864/900）

まずは数学の基礎固め

数学は高校2年生の段階では入試への基礎固めをすることがまず第一にやることです。 基本的には学校の学習と合わせて、 青チャートやフォーカスゴールドなどの網羅系問題集を解いていけば良いでしょう。

ここで気をつけるべきはこの様な網羅系の問題集は必ず一冊に絞ってやるということです。 青チャートもやってフォーカスゴールドもやって、 他の網羅系問題集もやって、だと時間がたくさんかかってしまいますし、 この様な網羅系の問題集は内容がかなり被っているのでどれか一冊を完璧にすれば他のものはやらなくて良いのです。 最も効率のよい方法としては例題だけを解いていく方法だと思います。

問題は初めから全部解ける必要はない

初めから自分で全部とくのはかなり大変なので、 はじめはどんどん答えを見ながらやって行くと良いと思います。 答えを見てその理屈の部分が分かれば良いので初めから全部を自分で解ける必要は全くないのです。 （むしろ初めから全部を自分で解ける人は存在しないと思って良いくらいだと思います。）

現状に余裕がある場合

現状余裕がある人向けに話をすると、 数学はできるだけ早く高校範囲を学び終えるのにこしたことはありません。 （もちろん、今学校などで習っている範囲の基礎がしっかりしているという前提がありますが。）

目安としては高校2年生の秋くらいまでは英語と数学にかなり力を割り当てて良いと思うので、 その時期くらいまでの間は余裕があるなら数学には時間をたっぷり割いて、 どんどん先の範囲を学習してしまうと良いと思います。

ただ、学校の学習と合わせて網羅系問題集をやっていくだけでほとんど全ての志望校に合格できるだけの 基礎力を受験生になるまでにつけることができますので 、これは本当に余裕があって、かつ現在習っている範囲の基礎がしっかり固まっている方だ けプラスアルファ的にやると良いと思います。

東大「医学部」「理三」合格者が実践した数学勉強法

基本的に数学を得意科目にするためには以上の勉強法を実践していただければ大丈夫です。

以下でご紹介するのはあくまで体験談です。 ここに掲載する意味は、全国のトップ進学校と言われる高校の生徒が実際の学校のカリキュラムや＋αとして 何をやっているのかを知りたいというご要望にお応えするためです。

この点をご了承の上ご覧ください。

都内トップ進学校出身者の数学勉強法

都内私立高校⇒東大理三現役合格講師 荻原（センター試験821/900）

基礎

学校の勉強をメインにやっていました。 因数分解や多項式の分野に関しては，学校側が出す計算問題を解くことによって， 身につけて行きました。

ここで，多く演習を積んだことによって， 文字式に対する扱いに慣れその後もつまずくことなく学習を続けられました。

幾何に関しては，学校でユークリッドの言論から始めたので特に参考にならないのですが， その中で定理の証明に多く触れたため，自分で証明を書くときの言葉遣いや論理展開を学ぶことができました。 特に学校以上の勉強をすることはなかったです。

標準

ひたすら典型問題を網3することに集中しました。 例題集をやっていたのですが，難易度的には青チャートくらいだったと思います。 解法の着想点から細かな計算までを何回も復習して， 同じような問題を見た時にその問題に関する知識を全て思い出せて， 手を止めることなく解けるようにしました。一問に合計2時間くらいは費やしていたと思います。

この段階の作業が受験数学の土台となったと感じています。 典型問題を完璧に身につけることで， 本番で典型題が出たときに時間が短縮できる他、 応用問題を典型題と結びつけることで解きやすくもなるし、定着しやすくなります。

過去問

東大過去問集を8年分解きました。 典型問題に結びつけることを意識して演習を行いました。 点数がブレブレだったので、どんなセットでも80点以上を取ることを目標にすることによって ある程度点数が落ち着きました。 過去問を解いている期間は高三で理科をメインにやっていたので，力の維持程度にやっていました。

センター試験

過去問を2年分解きました。

時期的なアドバイス

高一，高二で英語数学を固めて高三を理科に回すという鉄板のプランを建てる場合， 高一からしっかりと学校以外の勉強の強度を高めていくといいと思います。

高1の間に基礎，標準の問題を完璧にして，数三の基礎的な部分を終わらせ， 高二になって難しい問題に手を出し始めて基礎を復習しつつ進めて， 高三では演習のみにするというのが理想だと思います。

全国屈指の地方私立進学校出身者の数学勉強法

地方私立高校⇒東大理三現役合格講師 岡元（センター試験873/900）

学校のステップに従う

単元の説明・解説→教科書の練習問題→教科書傍用問題集→シグマベストor チャート式 の流れで全部の単元を終え、あとは数研出版の演習用の問題集をやっていた。 学校からの指示で、一対一対応を数Ⅲ以外やっていた。毎日数学には触れていた。

具体的な取り組み方

数学は、僕はまずは単元の中身を教科書にある基本的な練習問題をやりながらある程度理解をして、 その後教科書傍用問題集のたくさんの問題を何度か繰り返してその分野を定着させて計算力をつけました。

それを一通り教科書の全部の単元で終えてから、より難易度の高い演習問題に入りました。 数学の勉強は、まず初見の問題を解こうとして、 問題集で解けなかった問題に✖️印をつけ、できた問題に✔︎印をつけます。 それで✖️印のついた問題をまたしばらくしてから白い紙に自分で何も見ずに解こうとします。 それでできた問題には✔︎というチェックをつけて、できなかった問題には✖️というチェックをつけます。 それを繰り返していき、全部の問題に✔︎がつくようになるまでその問題集を繰り返していました。 その勉強法を全部の数学の教材にやっていました。

そうして基本的、典型的な問題をすべてマスターしていくことが重要だと思います。

実際に使っていた問題集・参考書

①教科書　②教科書傍用問題集　③チャート式＆シグマベスト　④一対一対応　⑤演習用問題集　⑥過去問　の６個で数学の勉強をしました。

① まず数学の新しい単元を勉強するときは教科書から入るものだと思います。教科書をしっかり読み、例題や練習問題を通じて基本を理解し、公式や定理がその証明から書いてあればそれも頭に入れた方がいいと思います。教科書レベルの基本を完璧にするというのが単元を勉強する上でのスタートだと思います。

② ①で教科書を勉強しても全てが本当に理解できているかは分からないですし、理解できていても問題が解けなければいけないので、その単元の練習問題をたくさん解くべきだと思います。たくさん練習をすることで理解が深まったり素早く解けるようになったりします。教科書傍用問題集には教科書より難しいレベルの問題も載っているので解ける問題のレベルも上がると思います。

③ ②と同時並行でもいいと思いますが、数学には各単元に基本例題、標準例題、発展例題があり、それらをすらすらと解けるようにならないといけません。僕は例題の解答を下の答えを見ずに自分で作れるようになるまで繰り返し練習していました。

④ ③と被っている部分も多いと思うのですが、僕は一対一対応の問題も③と同じようなやり方で勉強していました。

⑤ 数学は、結局入試の時に自分が今まで見たことの無いような問題を解けるようにならないといけないので、基本を頭に入れる作業だけでなく実際にいろんな問題を解いてみなければなりません。勉強してきたことをうまく組み合わせればほとんどの問題は解けるように作ってあるはずなので、なるべく答えを見ずに最後の答えまで出し切ろうとする練習は本番で問題が解けるようになるための練習になると思います。

⑥ 最後は、受ける大学によって問題の傾向が違うので、自分が受ける大学の入試問題をたくさん解くべきです。入試では、時間内に何点以上とるかが大事なので、過去問を解くときは模試のように時間を測ってどう解いていくか考える練習をたくさんするべきだと思います。

地方公立高校出身者の数学勉強法

地方公立高校⇒東大理三現役合格講師 岡田（センター試験844/900）

⾃分の出⾝が公⽴⾼校なので、公⽴⾼校の場合を書いていきます。

（１）基礎：教科書レベル

学校の授業は教科書をベースに進んでいくと思います。 なので、その教科書の使い⽅をまず述べたいと思います。 教科書の記述の中で特に重視すべきは『定義と定 理（とその証明）』です。 定義が重要なのは『（極論ですが）全ての問題が定義に帰着するから』です。 ま た、定義は定理を導いたり問題を解いたりするための前提 （英語でいうところのア ルファベットみたいなもの）なので形式・意味ともに暗記すべきです。

定理は主張・導出過程が重要です。が、主張はとりあえず覚えとく、導出過程も ⼀回は⽬を通しておく、 ぐらいで良いと思います。定理は問題を解いていくうちに 否応無く覚えてしまうものだし、 導出過程も当然重要ではありますが暗記するほど ではないからです。 （志望校で定理の導出がよく問われる場合はこの限りではないです。）

教科書を使った学習だとこうした定義・定理の意味を理解する（必要なら暗記する） ことを最優先に考えると良いと思います。

そして定理・定義が終わったら、忘れないうちに、 教科書傍⽤問題集などで演習すると良いと思います。 教科書傍⽤問題集は定理・定義の使い⽅を学ぶための本な ので、 定理・定義さえ分かっていれば（基本的には）解けるし、 時間を空けてから 演習すると定理・定義を頭に⼊れ直さないといけなくなり⼆度⼿間だからです。

また教科書傍⽤問題集は定理・定義の使い⽅を学ぶだけの本なので、何回も解き直す 必要はないです。 教科書で学んだ直後と定期考査前の２回で⼗分だし、 もっと⾔え ば2回⽬は1回⽬で間違えたところを中⼼に所々省きながら解くので⼗分だと思います。

以上が基礎レベルの勉強の仕⽅です。 これらは最低限、授業と並⾏して⾏っておくのが望ましいと思います。

（２）標準：⻘チャートレベル

次に、⻘チャートのような受験数学の定⽯を網羅した問題集の使い⽅を⾒て⾏き ましょう。 公⽴⾼校だと数３まで全部習い終えるのが⾼３の夏頃と遅めなので、 こ れらは可能な限り授業と並⾏して⾏うべきです。 （無理なら⻑期休暇中にまとめて ⽚付けるのもありだと思います。 ）

これらは考えて解くというよりは、『POINT』 とか『考え⽅』みたいな部分を理解して、 問題を解くための考え⽅を吸収するための本です。 なので基本的には考え⽅と解答の流れ（どのように⽴式するか）を読ん で理解し、 それが⾃分の中で常識になるまで繰り返し読み返す、という使い⽅をすべきでしょう。

ただ読む勉強だけでは計算⼒や解答作成能⼒が⾝につかないので、 時々問題を紙に書いて解く練習もするのが良いでしょう。 （ただし同じ時間だけ勉 強するなら、 書く勉強よりも読む勉強の⽅が定着しやすいのでメインは読む勉強が 良いと思います。）

この段階の学習を終える⽬安は、問題集の問題を⾒た瞬間に解 答の流れが頭に浮かぶレベルです。 この時点で全統模試や進研模試は全問完答も視野に⼊るはずです。

（３）応⽤：過去問

応⽤レベルに該当する問題集は⼭ほどありますが、最優先は志望校の過去問です。 志望校の傾向・難易度・時間制限を完全に反映している本は過去問だけだからです。

共通テスト後の30⽇程度で（そこまでに標準レベルが完璧になっていれ ば） 1⽇1年分弱消費するとしても25ヵ年分はこなせるので、 本格的にやり始めるのは共通テスト後でも⼤丈夫だと思います。 （欲を⾔えば標準レベルが⾝について から共通テスト前までに何年分か過去問を解いて、 傾向や現時点での⾃分の実⼒を把 握しておいた⽅が良いと思いますが。）

過去問演習のポイントは解いた後に、 なぜ 解けなかったのかをはっきりさせることです。 僕は⾃分が⾒落としやすいポイントや、うっかり使うのを忘れがちな解法をノートに書き留めて ⾃分の弱点やミスの傾 向を可視化できるようにしていました。 こうすることで⾃分の弱点を意識しながら 問題に当たれるようになるので、 問題演習も効果的なものになってくるからです。

また過去問演習から逆算して時間的に余裕があるようであれば、 他の問題集をや るのも良いと思います。 ここでの問題集の使い⽅としては、実践演習も兼ねて1 周⽬は書く勉強をメインに、 2周⽬以降は解答の流れを覚えてしまうために読む勉 強をメインに持ってくるのが良いと思います。 これも標準レベルの問題集と同様に 模範解答の流れがすぐに思い浮かぶレベルまで繰り返し 読み返すのがいいと思いま す。

以上が数学勉強法の概要です。 受験⽣1⼈1⼈にとってベストな勉強法とは、 ⾼校の進度や 数学の好き嫌いによって多少ずれがあると思います。 しかしどんな受験⽣でも『定理・定 義/標準レベルの徹底理解/過去問』が軸で、 かつ最も時間をかけてすべきだということは 共通していると思います。

また、逆にそこさえクリアすれば⼤抵の⼤学は合格するでしょう。 （実際には、ほとんどの受験⽣はこうしたことがクリアできていないから不合格になってしまうのです。）

したがって、この『軸』だけを集中的に勉強していくこの勉強法は必要⼗分なものだと思って います。 以上です。

あわせて読んでほしい数学勉強法のコンテンツ

以上の勉強法及び当塾の著書、
「受験の叡智」【受験戦略・勉強法の体系書】 ▶
「医学部」受験の叡智【受験戦略・勉強法の体系書】▶
と以下のコンテンツを読んでいただければ数学の勉強法についてこれ以上的確かつ優れた情報を得ている受験生はいない、と断言できます。

有効活用して医学部。難関大学合格をつかみ取ってください！

数学勉強法｜70項目と13動画で学ぶ数学対策

「難関大学合格までの数学最短ルートの対策と手順」 「数学問題集・参考書の使い方」「数学の問題演習を効率化させる方法」「数学の過去問の活用法」 「数学を攻略するツボ　東大トップ合格者の数学勉強法」 「東大理三合格者の数学の勉強のコツ」 「数学力を確実かつ大きく伸ばす秘密」 をまとめたコンテンツです。

相当な量になりますが数学勉強法を一気に学びたい、 数学力を徹底的につけたい、日々の数学の勉強を見直したいという方にはおすすめです。

【医学部受験】数学勉強法｜東大医学部合格講師30名超が受験対策を分析

全国のすべての医学部の問題を分析している当塾の30名超の東大医学部講師陣が書き下ろした勉強法記事を 医学部受験生のために医学部数学の勉強法として特化すべき部分を掲載したコンテンツです。

医学部数学で高得点を獲得することは医学部合格可能性を大きく上げることにつながります。 是非役立ててください。

数学勉強法を9つの動画で医学部（東大理3）合格者が解説！

数学の勉強法に関する当塾の無料動画をまとめて掲載したコンテンツです。東大理三合格講師が数学勉強法を解説しています。数学勉強法をとりあえず動画でという方はこちらをご覧ください。

数学の基礎固めの勉強法｜実力を伸ばす5つのポイント

数学は基礎固めの勉強なくして絶対に実力はつきません。 医学部を目指す受験生ほど基礎固めをまず重視してください。 数学の基礎固めの勉強法だけを抜き出したページです。

共通テスト数学の勉強法｜9割超への対策

共通テスト数学で高得点、9割超を獲得したい方は、 共通テスト数学の勉強法｜9割超への対策をご覧ください。

勉強法と共に必須となる数学対策の知識

ここまで読んできてくださった皆さんに、 多くの受験生が気づいていない合格するための数学勉強法、対策について最も大事なことをお伝えします。 もう一息です。最後まで読み切ってくださいね。

数学の勉強法というものは世間には沢山あります。 しかし的確性・質に大きな違いがある= その勉強法から得られる受験結果には雲泥の差が出る、 この現実と原因に気づいていますか？

数学の実力が伸びない受験界に隠された大きな要因

合格基準を満たしていない勉強法をいくら学ぼうが、 指導をいくら受けようがあなたの数学の実力は合格レベルまでは確実には伸びません。 合格はこの時点で運になってしまっているのです。 指導者がそもそも有していないもの、有していないレベルのものを教えることなど決して不可能、 したがってそれを受験生が得ることなど決してできないのです。

指導側に受験結果が伴っていなくても表面的に同じような勉強法を語ることは優れたものを剽窃していけば 誰でもできてしまいます。しかしそのようなものは本質を理解できていないゆえに必ず論理破たん、 論理矛盾があります。これを信じてしまうといくら勉強しても効率的に数学の実力はつきません。

数学力の絶対的な実力・質の差=結果の差

ここからは更なる核心にふれます。当塾が著書でも講座説明でも『圧倒的実力』という言葉に込めているメッセージの真意をご説明します。 まず下図をご覧ください。

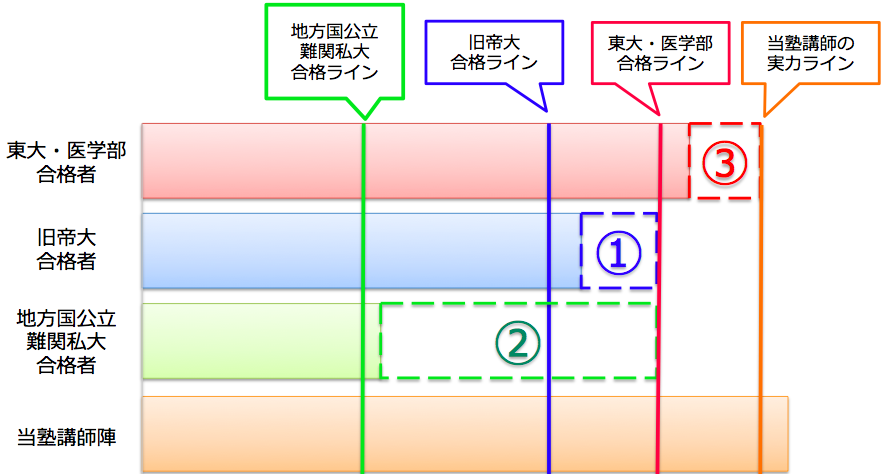
受験指導や勉強法を謳うものには様々なものがあります。 しかし、講師の受験結果・実力の差からみなさんが思っている以上に得られるものに大きな差が生じるという現実があることをどこまで理解できているでしょうか。

医学部や旧帝大及び早慶などの難関大理系に合格することは非常に難しいですよね。 なぜ難しいかといえばそこに合格するだけの知識、知識の本質的な理解、思考、エッセンスの抽出、効率的かつ優れた習得ノウハウを身につけること、自力で発見することが難しいからです。不合格という結果は合格するだけの知識、知識の本質的な理解、思考、エッセンスの抽出、効率的かつ優れた習得ノウハウを身につけること、自力で発見することが不可能だった、十分でなかったからです。ここまでは誰もが簡単にわかることだと思います。

また、そもそも医学部や難関理系を受験していなかったのなら自身で対策すらしていないのですから何もその人は有していません。医学部や難関理系に合格するための数学の優れた勉強法や対策、指導という点に関しては、たとえ東大合格者であっても文系合格者であれば的確なものは有していないのです。

では、上記のお話を指導する側からとらえてみてください。指導者になったからといって自身が実際に合格していない、対策していないにもかかわらず、医学部や旧帝大及び早慶などの難関大理系に合格するだけの数学の知識、知識の本質的な理解、思考、エッセンスの抽出、効率的かつ優れた習得ノウハウを教えることができるでしょうか？

医学部や難関理系に合格する知識、知識の本質的な理解、思考、エッセンスの抽出、効率的かつ優れた習得ノウハウというものを持っていなかったから合格していないのです。数学が得意科目ではなかったのです。 上図での①②の部分に得られなかったもの、得ていないもの、知らないもの、理解していないものが存在しているということです。 また、そもそも医学部や旧帝大レベルを受験していないのであればそのレベルに至る知識の本質的な理解、思考、エッセンスの抽出、ノウハウというものをそもそも知らない、正確に捉えることなど決してできないことは説明するまでもないことです。

一口に数学勉強法や対策と言っても大きな差がある

上図での①②の部分について 欠けている人の勉強法を参考にしたり、講義を受けたり、その人に質問をしたとして医学部や難関理系合格に必要な十分な知識、知識の本質的な理解、思考、エッセンスの抽出、ノウハウを満たしたものが得られるでしょうか。 教科や分野を問わず得ていくことが出来るでしょうか。 答えはノーなのです。合格基準を満たした数学勉強法や対策を十分な質とレベルで得ていけるなどということはありえないのです。そもそも持っていないもの、知らないものを教えることなど不可能だからです。

さらに、たとえ上記それぞれの合格ラインを超えていても、 ギリギリ合格の場合や同レベルの他の大学や学部を不合格になっている場合は ■■の部分についても知識、知識の本質的な理解、思考、エッセンスの抽出、ノウハウが欠けている、欠けている可能性が十分にあるという証拠なのです。さらに文系学部合格であるならば医学部や東大理系、さらには旧帝理系学部、早慶や難関私大理系の数学について合格レベルを超える本質的理解やエッセンスの抽出等のノウハウを持ち合わせていません。さらにつけ加えるなら同じ医学部合格者や東大・旧帝大理系合格者と一言でいってもその実力差はものすごく大きいという事実も知っておいてください。

以上の現実を非常にわかりやすい例でみなさんに問います。東大理三に合格していない人から東大理三合格に本当に必要な指導やノウハウを得ることが出来るでしょうか？ これは不可能であることは簡単にお分かりいただけると思います。あなたの志望校がどこであってもそれを『数段』超える実力をつけている人間から 数学勉強法や対策を学ぶことで初めて合格に必要なすべてを得ることが出来るのです。

世の中の数学勉強法の闇

受験生時代に一生懸命勉強して得られなかったものをその後に得るなどということはほぼ不可能です。 難関理系に合格すること、さらにはその上の旧帝大理系に合格すること、 さらにはその上の東大理系や医学部に合格することは非常に難しいことだったはずです。 それが指導者になったからと言って安易に得られるはずはないのです。 確かに表面的な知識は指導年数を重ねれば得ることはできます。しかし本質的理解やそれを前提とした思考、エッセンス、ノウハウの本当に優れたものの正体は事後的に安易に得られるほど薄っぺらいものではありません。 また、実際の試験を通じて合格という結果に実証されていない限りそれは役立つものではありません。 結果を出していなくてよいのならそれは誰でも主張できます。 仮にそれを事後的に本当に得たのであればその人の受験生時代の勉強法や勉強計画には重大な欠陥があったことになります。 要するにその部分で受験生としての限られた時間的制約の中で本当に優れたものを得ていない、 よってその部分の本当に優れたものを教えることはできないという事実があるのです。

数学の入試問題の性質から導かれる致命的な現実

医学部や難関理系と言えども基礎標準知識を前提とした範囲の問題を取りこぼしなく解答できれば確実に合格できます。 例えば、東大の問題ですら基礎標準知識の本質的な理解とその使いこなしで合格点を遥かに超える得点を獲得できるように作られています。 さらに私立医大や私大理系であっても基礎標準知識の本質的理解を用いて基礎標準知識問題を取り切れば合格点を超えます。この事実の意味をよく考えてください。ここに指導側の受験結果の差から導かれる数学勉強法の質や対策、さらには指導における重大な秘密が隠れています。

基礎標準知識の本質的な理解とその使いこなしが出来ればどこの大学にも合格できる、ということは難関理系に合格出来なかったという事実は、どの大学でも合格のために必須となる基礎標準知識の本質的理解とその使いこなしの術が足りていない、空白の部分があるという事実を示します。これを指導者の側から考えてみてください。圧倒的結果を出している人間しか十分に指導できる基礎標準知識の本質的理解とその使いこなしの術は網羅的に有していないということなのです。ここに至っていない人は基礎標準知識の範囲ですら的確なものを教えることができない・曖昧な部分・空白の部分が多々存在するという現実を意味するのです。あなたの志望大学がどこであっても必ず出題される基礎標準知識の範囲において存在するのです。これが数学の勉強法や対策、さらには指導にすべて影響してくるのです。ここに気づかないことは恐ろしいことではないですか？

受験結果の真実を分析した究極の数学対策

以上の受験結果の真実=各教科を大学受験最高のレベルと網羅性を満たして教えることが出来る⇒ これによって本当に的確かつ実力を確実にあげる勉強法（勉強計画や受験戦略）を初めて教えることが出来る という事実を分析して東大医学部・理三合格講師30名超を有しその叡智を結集して数学勉強法をはじめ 全教科の勉強法や勉強計画、受験戦略、受験指導をご提供しているのが叡学会（株）合格の天使です。 講師の実力差によって得られるものが全く異なるという現実を十分理解したうえで、 数学勉強法や対策というものをしっかりと考えて合格へ向かってください！ 本気で数学の実力をあげたいなら、受講云々は抜きにして、本当に優れた指導やノウハウ、方法論というものがいかなるものなのかを 公式サイトのトップページから是非ご覧ください。

圧倒的結果に実証されている優れた数学勉強法を、医学部や難関大学を目指すお友達やお知り合いにも教えてあげてください。 以下のシェアボタンを押せば簡単にシェアできます。